B=4+4^3+4^5+...+4^49
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
T
1
S
29 tháng 3 2023
\(B=\dfrac{4}{1\times3}+\dfrac{4}{3\times5}+\dfrac{4}{5\times7}+...+\dfrac{4}{47\times49}+\dfrac{4}{49\times51}\)
\(=2\times\left(\dfrac{2}{1\times3}+\dfrac{2}{3\times5}+\dfrac{2}{5\times7}+...+\dfrac{2}{47\times49}+\dfrac{2}{49\times51}\right)\)
\(=2\times\left(1-\dfrac{1}{3}+\dfrac{1}{3}-\dfrac{1}{5}+\dfrac{1}{5}-\dfrac{1}{7}+...+\dfrac{1}{47}-\dfrac{1}{49}+\dfrac{1}{49}-\dfrac{1}{51}\right)\)
\(=2\times\left(1-\dfrac{1}{51}\right)\)
\(=2\times\dfrac{50}{51}\)
\(=\dfrac{100}{51}\)
NT
1
2 tháng 3 2022
a: =-2/49-5/3+2/49=-5/3
b: \(=\dfrac{5\cdot4^{15}\cdot9^9-4\cdot3^{20}\cdot8^9}{5\cdot2^9\cdot6^{19}-7\cdot2^{29}\cdot27^6}\)
\(=\dfrac{5\cdot2^{30}\cdot3^{18}-3^{20}\cdot2^{27}\cdot2^2}{5\cdot2^9\cdot2^{19}\cdot3^{19}-7\cdot2^{29}\cdot3^{18}}\)
\(=\dfrac{5\cdot2^{30}\cdot3^{18}-3^{20}\cdot2^{29}}{5\cdot2^{28}\cdot3^{19}-7\cdot2^{29}\cdot3^{18}}\)
\(=\dfrac{2^{29}\cdot3^{18}\left(2\cdot3-3^2\right)}{2^{28}\cdot3^{18}\left(5\cdot3-7\cdot2\right)}=2\cdot\dfrac{6-9}{15-14}=2\cdot\left(-3\right)=-6\)
NT
1
NP
0
VN
Võ Ngọc Phương
VIP
18 tháng 7 2023
\(\dfrac{11}{49}\times\dfrac{1}{2}+\dfrac{11}{49}:\dfrac{5}{4}-\dfrac{11}{49}\times\dfrac{3}{4}\)
\(=\dfrac{11}{49}\times\dfrac{1}{2}+\dfrac{11}{49}\times\dfrac{4}{5}-\dfrac{11}{49}\times\dfrac{3}{4}\)
\(=\dfrac{11}{49}\times\left(\dfrac{1}{2}+\dfrac{4}{5}-\dfrac{3}{4}\right)\)
\(=\dfrac{11}{49}\times\left(\dfrac{10}{20}+\dfrac{16}{20}-\dfrac{15}{20}\right)\)
\(=\dfrac{11}{49}\times\dfrac{11}{20}\)
\(=\dfrac{121}{980}\)
Chúc bạn học tốt
18 tháng 7 2023
`@` `\text {Ans}`
`\downarrow`
\(\dfrac{11}{49}\times\dfrac{1}{2}+\dfrac{11}{49}\div\dfrac{5}{4}-\dfrac{11}{49}\times\dfrac{3}{4}\)
`=`\(\dfrac{11}{49}\times\dfrac{1}{2}+\dfrac{11}{49}\times\dfrac{4}{5}-\dfrac{11}{49}\times\dfrac{3}{4}\)
`=`\(\dfrac{11}{49}\times\left(\dfrac{1}{2}+\dfrac{4}{5}-\dfrac{3}{4}\right)\)
`=`\(\dfrac{11}{49}\times\dfrac{11}{20}\)
`=`\(\dfrac{121}{980}\)
K
0
HG
0
18 tháng 6 2021
`a)\sqrt{9-4sqrt5}-sqrt5`
`=sqrt{5-2.2sqrt5+4}-sqrt5`
`=sqrt{(sqrt5-2)^2}-sqrt5`
`=|\sqrt5-2|-sqrt5`
`=sqrt5-2-sqrt5=-2`
`b)\sqrt{7-4sqrt3}+sqrt{4-2sqrt3}`
`=\sqrt{4-2.2sqrt3+3}+\sqrt{3-2sqrt3+1}`
`=sqrt{(2-sqrt3)^2}+sqrt{(sqrt3-1)^2}`
`=|2-sqrt3|+|sqrt3-1|`
`=2-sqrt3+sqrt3-1=1`
`c)(x-49)/(sqrtx-7)(x>=0,x ne 49)`
`=((sqrtx-7)(sqrtx+7))/(sqrtx-7)`
`=sqrtx+7`
`d)\sqrt{4+2\sqrt3}-\sqrt{13+4sqrt3}`
`=\sqrt{3+2sqrt3+1}-\sqrt{12+2.2sqrt3+1}`
`=sqrt{(sqrt3+1)^2}-\sqrt{(2sqrt3+1)^2}`
`=sqrt3+1-2sqrt3-1=-sqrt3`
`e)2+sqrt{17-4sqrt{9+4sqrt{45}}}`(câu này hơi sai)
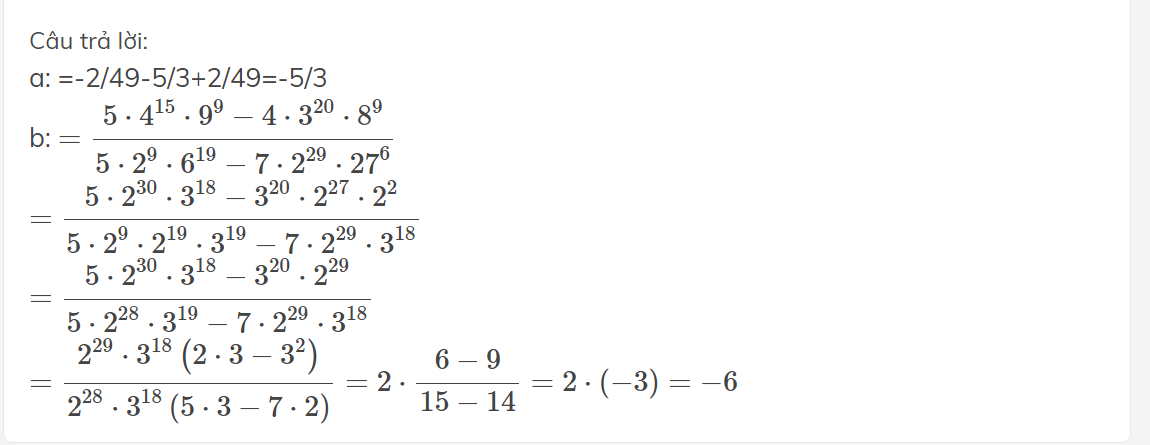
B = 4 + 43 + 45 +.....+449
42.B = 43 + 45+......+449 + 451
16B - B = 451 - 4
15B = ( 451-4)
B = (451 - 4): 16