tìm x biết : 2x3=(x-1)3
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
11 tháng 7 2023
\(3^{x+1}+3^{x+2}=2^2.3^4\)
\(3^{x+1}+3.3^{x+1}=4.81\)
\(4.3^{x+1}=4.81\)
\(3^{x+1}=81=3^4\)
\(x+1=4\Rightarrow x=3\)
DD
Đoàn Đức Hà
Giáo viên
25 tháng 5 2021
b) \(\frac{1}{1.3}+\frac{1}{3.5}+\frac{1}{5.7}+...+\frac{1}{2013.2015}\)
\(=\frac{1}{2}\left(\frac{2}{1.3}+\frac{2}{3.5}+\frac{2}{5.7}+...+\frac{2}{2013.2015}\right)\)
\(=\frac{1}{2}\left(\frac{3-1}{1.3}+\frac{5-3}{3.5}+\frac{7-5}{5.7}+...+\frac{2015-2013}{2013.2015}\right)\)
\(=\frac{1}{2}\left(1-\frac{1}{3}+\frac{1}{3}-\frac{1}{5}+\frac{1}{5}-\frac{1}{7}+...+\frac{1}{2013}-\frac{1}{2015}\right)\)
\(=\frac{1}{2}\left(1-\frac{1}{2015}\right)=\frac{1007}{2015}\)
Phương trình tương đương với:
\(\frac{1007X}{2015}=\frac{4}{2015}\Leftrightarrow X=\frac{4}{1007}\)
DD
Đoàn Đức Hà
Giáo viên
25 tháng 5 2021
c) \(\frac{x+1}{2015}+\frac{x+2}{2016}=\frac{x+3}{2017}+\frac{x+4}{2018}\)
\(\Leftrightarrow\frac{x+1}{2015}-1+\frac{x+2}{2016}-1=\frac{x+3}{2017}-1+\frac{x+4}{2018}-1\)
\(\Leftrightarrow\frac{x-2014}{2015}+\frac{x-2014}{2016}=\frac{x-2014}{2017}+\frac{x-2014}{2018}\)
\(\Leftrightarrow x-2014=0\)
\(\Leftrightarrow x=2014\)
CM
23 tháng 6 2017
Chọn C
Ta có: P(x) + Q(x) = x3+ x2+ 2x-1
⇒ Q(x) = (x3 + x2 + 2x-1) - P(x)
= 2x3 + 4x2 - 8x - 3.
25 tháng 4 2015
\(720:\left(x\times2+x\times3\right)=2\times3\)
\(720:\left(x\times5\right)=6\)
\(x\times5=720:6\)
\(x\times5=120\)
\(x=120:5\)
\(x=24\)
22 tháng 7 2023
3x+25=26x22+2x30
3x+25=26x4+2
3x+25=106
3x=106-25=81
3x=34
⇒ x=4
24 tháng 4 2023
f'(x)=2*3x^2+3*2*(a+2)*x+6a^2
=6x^2+6x(a+2)+6a^2
Δ=(6a+12)^2-4*6*6a^2
=36a^2+144a+144-144a^2
=-108a^2+144a+144
f'(x)>0 với mọi x
=>-108a^2+144a+144<0
=>a<-2/3; a>2
f'(-1)=6
=>6*(-1)^2+6*(-1)*(a+2)+6a^2=6
=>6a^2+6-6a-12=6
=>6a^2-6a-12=0
=>a^2-a-2=0
=>a=2(loại) hoặc a=-1(nhận)
PN
0
CB
2
HT
25 tháng 7 2015
\(\frac{1}{1.2}+\frac{1}{2.3}+\frac{1}{3.4}+.....+\frac{1}{x\left(x+1\right)}=\frac{99}{100}\)
\(1-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+.....+\frac{1}{x}-\frac{1}{x+1}=\frac{99}{100}\)
\(1-\frac{1}{x+1}=\frac{99}{100}\)
=> \(\frac{1}{x+1}=1-\frac{99}{100}=\frac{1}{100}\)
=> x+1 = 100
=> x = 100 - 1
=> x = 99
K
1
14 tháng 6 2015
\(\frac{1}{2.3}+\frac{1}{3.4}+...+\frac{1}{x.\left(x+1\right)}=\frac{299}{600}\)
\(\Rightarrow\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{x}-\frac{1}{x+1}=\frac{299}{600}\)
\(\Rightarrow\frac{1}{2}-\frac{1}{x+1}=\frac{299}{600}\)
\(\Rightarrow\frac{1}{x+1}=\frac{1}{2}-\frac{299}{600}\)
\(\Rightarrow\frac{1}{x+1}=\frac{1}{600}\)
\(\Rightarrow x+1=600\)
\(\Rightarrow x=600-1\)
\(\Rightarrow x=599\)
\(Vậy\) \(x=599\)
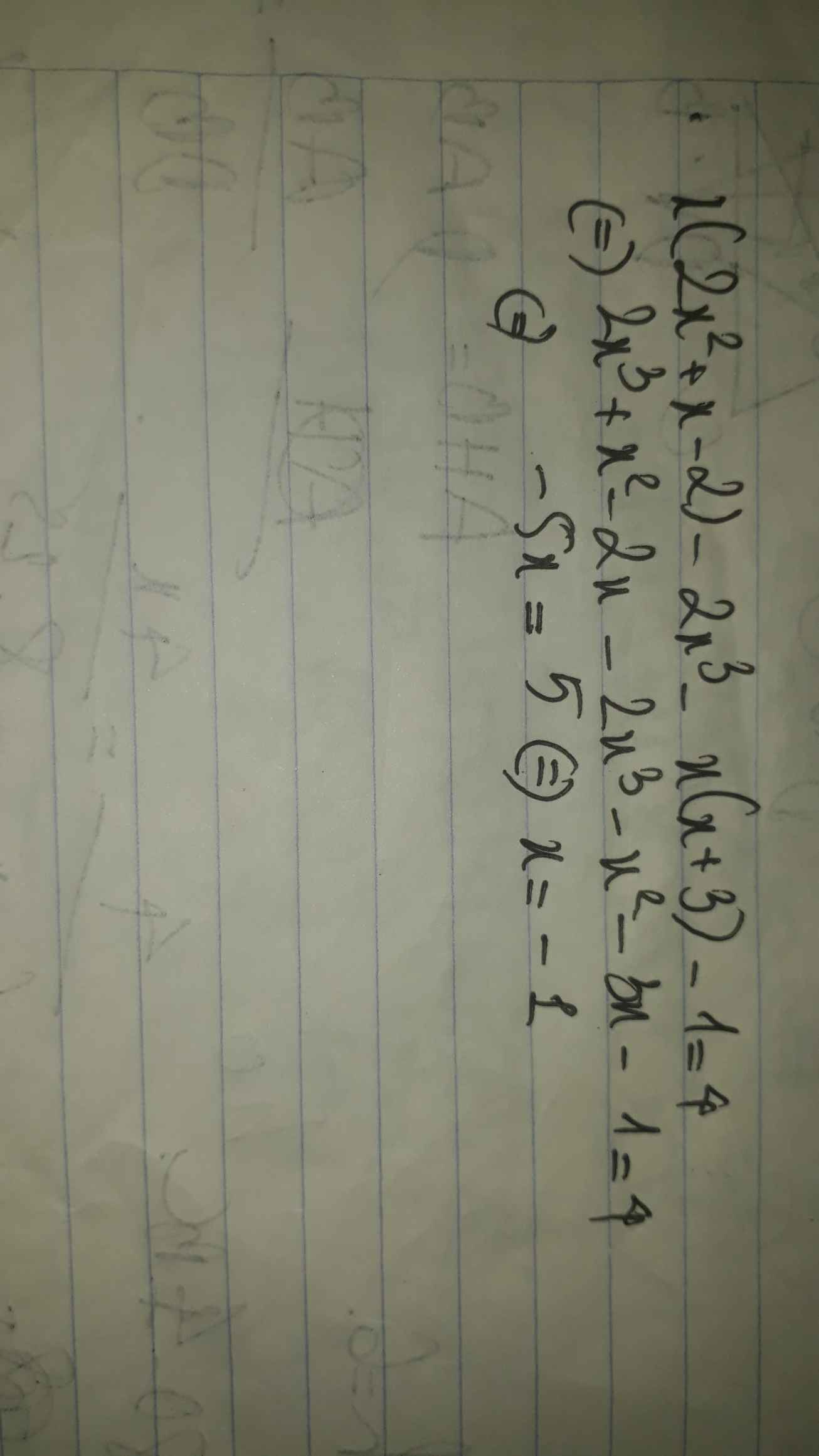
ờ, thế để tôi li ke cho
\(2x^3=\left(x-1\right)^3\Leftrightarrow2x^3-x^3+3x^2-3x+1=0\) (Khai chuyển hằng đẳng thức và chuyển vế luôn)
\(\Leftrightarrow x^3+3x^2-3x+1=0\) Dùng máy tính cầm tay mà bấm ra nghiệm