Tìm giá trị nhỏ nhất của P=2+x-x^2 (áp dụng hằng đẳng thức)
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
26 tháng 12 2022
Cả 2 biểu thức này đều ko tồn tại GTNN
GTNN chỉ tồn tại khi có thêm điều kiện, với \(\dfrac{x^2}{x+3}\) thì điều kiện là \(x>-3\), còn \(\dfrac{x^2}{x-2}\) thì điều kiện là \(x>2\)
TM
7 tháng 7 2017
bạn nói với mình điều kiện x>2 vậy làm như sau:
Đặt:\(A=\frac{3x-x^2-18}{x-2}=-\frac{x^2-3x+18}{x-2}=-\frac{x^2-4x+4+x-2+16}{x-2}\)
\(=-\frac{\left(x-2\right)^2+\left(x-2\right)+16}{x-2}\)\(=-\left(x-2+1+\frac{16}{x-2}\right)\)
Áp dụng bđt Cô si cho 2 số dương ta được: \(x-2+\frac{16}{x-2}\ge2\sqrt{\left(x-2\right).\frac{16}{x-2}}=8\)
=>\(x-2+\frac{16}{x-2}+1\ge9\)=>\(A=-\left(x-2+1+\frac{16}{x-2}\right)\le-9\)
=> maxA=-9 <=> x=6
5 tháng 7 2018
a) Ta có: \(A=4x^2-12x+15=\left(2x-3\right)^2+6\)
Vì \(\left(2x-3\right)^2\ge0\left(\forall x\in Z\right)\)
\(\Rightarrow A=\left(2x-3\right)^2+6\ge6\)
Dấu "=" xảy ra \(\Leftrightarrow2x-3=0\Leftrightarrow x=\frac{3}{2}\)
Vậy Amin = 6 khi và chỉ khi x = 3/2
b) \(B=x^2-x+1=x^2-2.x.\frac{1}{2}+\left(\frac{1}{2}\right)^2+\frac{3}{4}\)
\(=\left(x-\frac{1}{2}\right)^2+\frac{3}{4}\ge\frac{3}{4}\)
Dấu "=" xảy ra <=> x - 1/2 = 0 <=> x = 1/2
Vậy Bmin = 3/4 khi và chỉ khi x = 1/2
28 tháng 8 2019
bạn kham khảo link : https://olm.vn/hoi-dap/detail/88594630023.html
CM
2 tháng 7 2019
Điều kiện x ≠ 2 và x ≠ 0
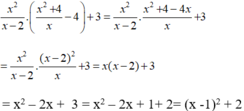
Vì x - 1 2 ≥ 0 nên x - 1 2 + 2 ≥ 2 với mọi giá trị của x.
Khi đó giá trị nhỏ nhất của biểu thức bằng 2 khi x = 1.
Vậy biểu thức đã cho có giá trị nhỏ nhất bằng 2 tại x = 1.
sai, parabol úp
cái này đáng ra là tìm giá trị lớn nhất chứ không phải nhỏ nhất
p = 2 + x - x2
P = -x2 + x + 2
P = - ( x2 - 2. \(\dfrac{1}{2}\)x + \(\dfrac{1}{4}\)) + \(\dfrac{9}{4}\)
P = - (x - \(\dfrac{1}{2}\))2 + \(\dfrac{9}{4}\)
- ( x - 1/2 ) 2 ≤ 0 ⇔ p ≤ \(\dfrac{9}{4}\)⇔ P(max) = 9/4 dấu = xảy ra khi x = 1/2