Tìm một số có 2 chữ số biết rằng khi đảo ngược hai chữ số đó thì được số mới bé hơn số ban đầu 45 đơn vị. Tìm số ban đầu. Mình biết kq nhưng không biết cách giải :v
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Gọi số cần tìm là abc; abc viết theo thứ tự đảo ngược lại có dạng là cba
Theo đề bài, ta có:
cba - abc = 792
c x 100 + b x 10 + a - a x 100 + b x 10 + c = 792
c x 100 - c + b x 10 - b x 10 + a - a x 100 = 792
c x 99 + a - a x 100 = 792
c x 99 + a = 792 + a x 100
c x 99 = 792 + a x 100 - a
c x 99 = 792 + a x 99
c x 99 - a x 99 = 792
( c - a ) x 99 = 792
c - a = 792 : 99 = 8
Ta có: cab
- abc
792
Xét a và c : c - a = 8 nhưng trong phép tính c - a = 7 => đây là phép trừ có nhớ và a < c nên phải lấy 1a - c = 2; nhớ 1 sang b ở số trừ . Nếu c lớn nhất = 9 thì a = 1 ta có: 11 - 9 = 2 ( đúng )
=> c = 9; a = 1. Ta có:
9b1
- 1b9
792
=> b = 0 để b - ( b + 1 ) có nhớ. Ta có:
901 - 109 = 792 Đ
Vậy số cần tìm là 109
số đó là: 195
(ko biết cách giải, tại mình quen ngồi mò số)

Gọi số cần tìm có dạng là \(\overline{ab}\)
2 lần chữ số hàng chục bé hơn chữ số hàng đơn vị là 1 nên b-2a=1
Nếu viết số đó theo thứ tự ngược lại thì được một số mới với tổng của số mới và số ban đầu là 143
=>\(\overline{ab}+\overline{ba}=143\)
=>11a+11b=143
=>a+b=13
Do đó, ta có hệ phương trình:
\(\left\{{}\begin{matrix}-2a+b=1\\a+b=13\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}-3a=-12\\a+b=13\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a=4\\b=9\end{matrix}\right.\)

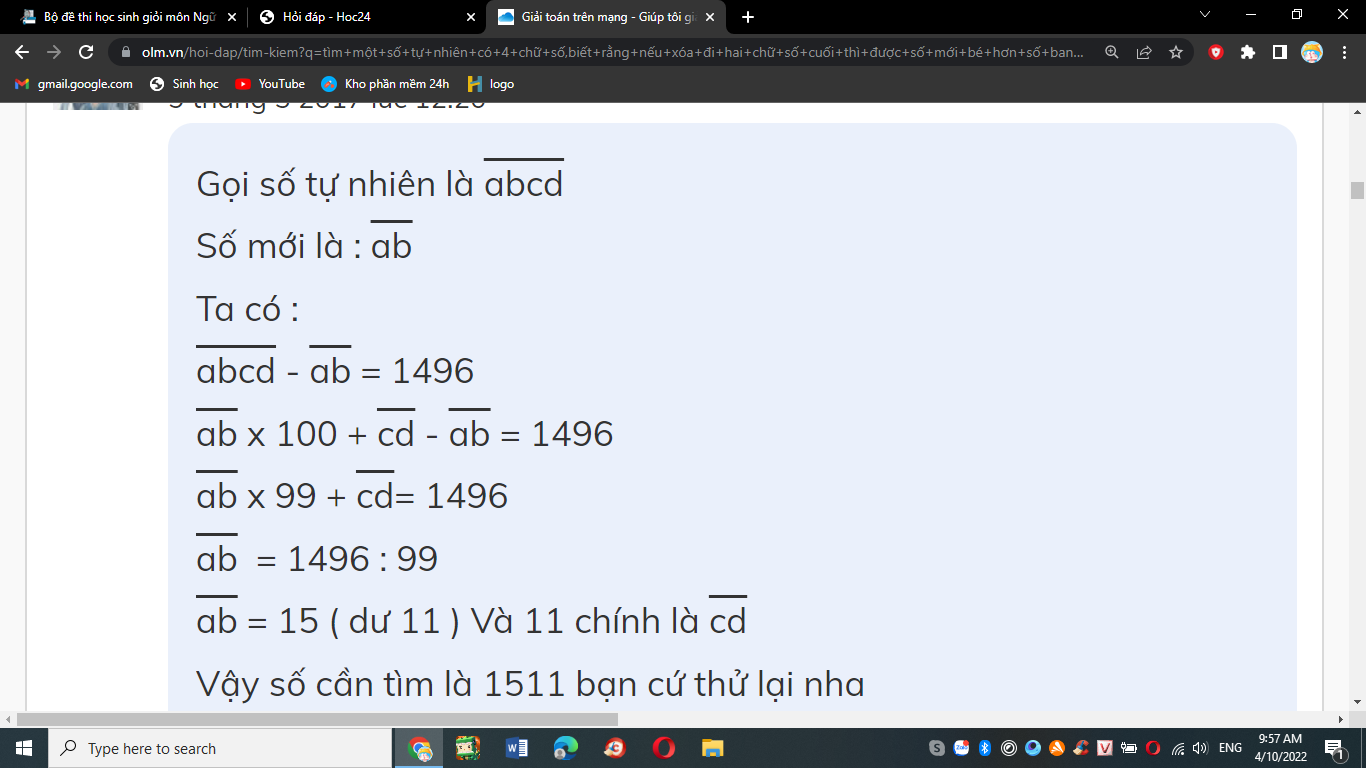
Gọi số tự nhiên là abcd
Số mới là : ab
Ta có :
abcd - ab = 1496
ab x 100 + cd - ab = 1496
ab x 99 + cd= 1496
ab = 1496 : 99
ab = 15 ( dư 11 ) Và 11 chính là cd
Vậy số cần tìm là 1511 bạn cứ thử lại nha
Gọi số tự nhiên là abcd
Số mới là : ab
Ta có :
abcd - ab = 1496
ab x 100 + cd - ab = 1496
ab x 99 + cd= 1496
ab = 1496 : 99
ab = 15 ( dư 11 ) Và 11 chính là cd
Vậy số cần tìm là 1511 bạn cứ thử lại nha

Lời giải:
Gọi số cần tìm là $\overline{ab}$. Điều kiện: $a,b$ là số tự nhiên; $a,b\leq 9; a\neq 0$
Theo bài ra ta có:
$\overline{a1b}=8\times \overline{ab}+14$
$a\times 100+10+b=8\times (10\times a+b)+14$
$a\times 100+10+b=80\times a+8\times b+14$
$20\times a-4=7\times b$
Vì $20\times a-4$ chia hết cho $4$ nên $7\times b$ chia hết cho $4$
Suy ra $b$ chia hết cho $4$. Do đó $b$ có thể có giá trị $0;4;8$
Nếu $b=0$ thì $20\times a-4=7\times 0=0$
$20\times a=4$
$a=\frac{1}{5}$ (loại)
Nếu $b=4$ thì $20\times a-4=7\times 4=28$
$20\times a=28+4=32$
$a=32:20$ không là số tự nhiên (loại)
Nếu $b=8$ thì $20\times a-4=7\times 8=56$
$20\times a=60$
$a=3$ (thỏa mãn)
Vậy số cần tìm là $38$
Gọi số cần tìm là ab ( a khác b ) Ta có:
aa (b-1) b = 91ab
1100a + 11b - 10 = 910a + 91b
=> 19a = 8b + 1
8b là số chẵn nên 8b = 1 là số lẻ => 19a là số lẻ => a lẻ b ≤≤ 9 => 8b + 1 ≤≤ 73 => a = 73 : 19
=> a = 1,3
Nếu a = 1 => b = 18 : 8 = 2,25 ( loại )
Nếu a = 3 => b = 7. Số phải tìm là 37

Ta gọi số tự nhiên cần tìm là abcd, 2 chữ số đã xóa đi là cd. Ta có:
abcd - ab = 2688
ab x 100 + cd - ab = 2688
(ab x 100 - ab) + cd = 2688
ab x 99 + cd = 2688
ab x 99 = 2688 - cd
=> 2688 : 99 = ab (dư cd)
Mà 2688 : 99 = 27 (dư 15). Vậy số cần tìm là 2715.
Đáp số: 2715

Gọi số đó là \(\overline{ab}\left(a\inℕ^∗,a\le9;b\inℕ,b\le9\right)\)
Chữ số hàng chục hơn chữ số hàng đơn vị là 5 nên ta có phương trình \(a-b=5\)(1)
Ta có \(\overline{ab}=10a+b\), khi đảo ngược thứ tự của hai chữ số, ta được số mới là \(\overline{ba}=10b+a\)
Vì số mới bằng \(\frac{3}{8}\)số ban đầu nên ta có phương trình \(10b+a=\frac{3}{8}\left(10a+b\right)\)
\(\Leftrightarrow80b+8a=30a+3b\)\(\Leftrightarrow22a-77b=0\)\(\Leftrightarrow2a-7b=0\)(2)
Từ (1) và (2) ta có hệ phương trình \(\hept{\begin{cases}a-b=5\\2a-7b=0\end{cases}}\Leftrightarrow\hept{\begin{cases}7a-7b=35\\-2a+7b=0\end{cases}}\Leftrightarrow\hept{\begin{cases}5a=35\\a-b=5\end{cases}}\)\(\Leftrightarrow\hept{\begin{cases}a=7\\b=2\end{cases}}\)
Vậy số cần tìm là 72
đã biết kq thì phải biết cách làm chứ