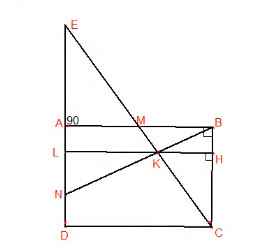
Cho hcn ABCD có dtich là 2020. Gọi M là trung điểm AB, và điểm N thuộc cạnh AD sao cho AN=2AD. CM và BN cắt nhau tại K. Tính dtich tam giác KBC
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NN
Nguyễn Ngọc Anh Minh
CTVHS
VIP
23 tháng 11 2023
2 tam giác AMK và tg BMK có
AM=BM; có chung đường cao từ K->AB nên
\(S_{AMK}=S_{BMK}=\dfrac{1}{2}S_{BKA}=\dfrac{1}{2}x50=25cm^2\)
2 tam giác ABN và tam giác CBN có chung đường cao từ B->AC nên
\(\dfrac{S_{ABN}}{S_{CBN}}=\dfrac{AN}{NC}=\dfrac{1}{2}\)
Hai tg ABN và tg CBN có chung BN nên
\(\dfrac{S_{ABN}}{S_{CBN}}=\) đường cao từ A->BN / đường cao từ C->BN \(=\dfrac{1}{2}\)
Hai tg BKA và tg BKC có chung BK nên
\(\dfrac{S_{BKA}}{S_{BKC}}=\) đường cao từ A->BN / đường cao từ C->BN \(=\dfrac{1}{2}\)
\(\Rightarrow S_{BKC}=2xS_{BKA}=2x50=100cm^2\)
\(\Rightarrow S_{BMC}=S_{BMK}+S_{BKC}=25+100=125cm^2\)
Hai tg BMC và tg AMC có chung đường cao từ C->AB nên
\(\dfrac{S_{BMC}}{S_{AMC}}=\dfrac{BM}{AM}=1\Rightarrow S_{BMC}=S_{AMC}=125cm^2\)
\(\Rightarrow S_{ABC}=S_{BMC}+S_{AMC}=125+125=250cm^2\)
22 tháng 9 2019
bn tự kẻ hình nha!
a) ta có: AB = DC ( ACBD là hình bình hành)
----> BM = CN ( = 1/2. AB = 1/2 . DC)
mà BM // CN
-----> BMNC là h.b.h
b) xét tam giác AMD và tam giác CNB
có: AM = CN ( = 1/2.AB = 1/2.CD)
AD = BC (gt)
^DAM = ^NCB (gt)
-----> tg AMD = tg CNB (c-g-c)
-----> DM = NB ( 2 cạnh t/ ư)
c) AN cắt DM tại I, MC cắt BN tại K. chứng minh : AC,BD,MN,IK
bài làm
Gọi AC cắt DB tại E
ta có: tg AMD = tg CNB (cmt)
-----> ^AMD = ^CNB
mà ^AMD = ^MDN ( AB//DC)
-----> ^CNB = ^MDN
mà ^CNB, ^MDN nằm ở vị trí đồng vị
-----> DM// BN
và DM = BN (pb)
-----> DMBN là h.b.h
-------> BD cắt MN tại E ( do 2 đường chéo của h.b.h cắt nhau tại trung điểm của mỗi đường)
tương tự bn cx chứng minh: MINK là h.b.h ( MI = NK = 1/2.DM = 1/2.BN)
-----> MN cắt IK tại E
------------> AC,BD, MN,IK đồng quy tại E
lx
lx