Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

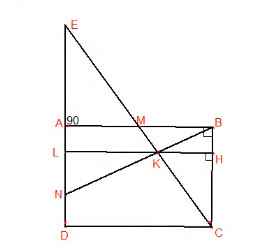
A B C D N E M 1 2
Mk chỉ nêu cách làm bạn tự triển khai nha!
CM \(\Delta ADC=\Delta CBE (g.c.g)\) (*)
(\(\angle C_1=\angle C_2\) cùng phụ với \(\angle ACB\))
\(\Rightarrow AC=CE\Rightarrow \Delta ACE \) cân tại C
\(\Rightarrow AB=CE\)
Từ (*) suy ra:
\(S_{ANEC}=S_{ACE}+S_{ANE}=S_{ABCD}+S_{ANE}\)
\(=\dfrac{1}{2}AB^2+\dfrac{1}{2}NA.2AB=\dfrac{1}{2}AB(AB+2NA)\)
Mà \( S_{ANCE}=\dfrac{15}{8} S_{ABCD}\) \(\Rightarrow \dfrac{15}{8}.\dfrac{1}{2} AB^2=\dfrac{1}{2}.AB(2AN+AB)\)
\(\Rightarrow 2AN+AB=\dfrac{15}{8}AB\) \(\Rightarrow \dfrac{NA}{AB}=\dfrac{7}{16}\)
CM \(\Delta NAM \) đồng dạng với \(\Delta CBM\) \((g.g)\)
\(\Rightarrow \dfrac{NA}{AB}=\dfrac{NA}{BC}=\dfrac{AM}{MB}=\dfrac{7}{16}\)
Vậy cần lấy M sao cho \(\dfrac{AM}{MB}=\dfrac{7}{16}\)

đặt MA= x (cm)
tam giác ABC cân nên : 12-x
diện tích hình bình hành MNCP là : MP.MA = (12-x)x
diện tích bằng 32cm vuông , nê ta có phương trình:
x^2 -12x +32 = 0
giải pt ta được x1= 4 , x2 =8
vậy M cách A là 4cm hoặc 8cm.