cho tam giác ABC có BC = 12cm , AC = 5cm , AB = 13cm . Chọn khẳng định đúng
A . tam giác ABC là tam giác vuông tại A
B. tám giác ABC là tam giác nhọn
C. tam giác ABC là tam giác vuông tại C
D . tam giác ABC là tam giác tù
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
20 tháng 6 2019
( cot C = tan B = 4 3 vì góc B và góc C là hai góc phụ nhau)
Áp dụng hệ thức về cạnh và hình chiếu trong tam giác vuông ta có:
A B 2 = B H . B C ⇒ B H = A B 2 B C = 12 2 20 = 7,2 ( c m )
CM
26 tháng 6 2019
a) Đúng. Khi đó, ∆ABC = ∆FDE ( g.c.g)
b) Sai;
c) Đúng.
+)Vì ta có: ∠A + ∠B +∠C = 180º ( tổng ba góc của tam giác).
Và ∠D + ∠E + ∠F = 180º ( tổng ba góc của tam giác)
+) Lại có; ∠B = ∠D; ∠C = ∠E nên ∠A = ∠F
+) Kết hợp giả thiết suy ra: ∆ABC = ∆ FDE ( g.c.g)
CM
22 tháng 10 2018
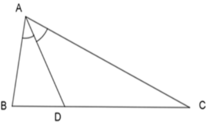
Vì AD là đường phân giác của tam giác ABC nên: A B A C = B D D C
Theo bài, ta có: AC = 2AB ⇒ A B A C = 1 2 ⇒ B D D C = 1 2 hay (I) đúng
Lại có: B D D C = 1 2 ⇒ B D B C = B D D C + B D = 1 2 + 1 = 1 3 nên (III) sai.
⇒ D C B C = B C − B D B C = 1 − B D B C = 1 − 1 3 = 2 3
hay (II) đúng
Vậy chỉ có 2 khẳng định đúng.
Đáp án: D
CM
15 tháng 1 2017
Chọn A.
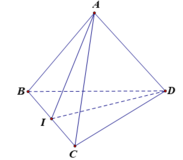
+) Tam giác ABC cân tại A có AI là đường trung tuyến nên đồng thời là đường cao: AI ⊥ BC (1)
+) Tam giác BCD cân tại D có DI là đường trung tuyến nên đồng thời là đường cao: DI ⊥ BC (2)
- Từ (1) và (2) suy ra BC ⊥ (ADI).
C
C