Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
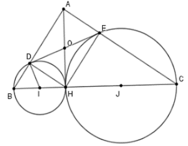
Gọi I, J lần lượt là trung điểm của BH và CH.
Để chứng minh DE là tiếp tuyến của đường tròn tâm I đường kính BH ta chứng minh ID ⊥ DE hay 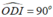
Vì D, E lần lượt thuộc đường tròn đường kính BH và HC

Nên DE là tiếp tuyến của đường tròn đường kính BH
Từ chứng minh trên suy ra các phương án B, C, D đúng

Chọn đáp án A
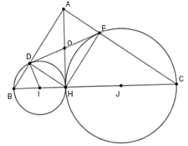
Gọi I, J lần lượt là trung điểm của BH và CH.
Để chứng minh DE là tiếp tuyến của đường tròn tâm I đường kính BH ta chứng minh ID ⊥ DE hay 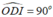
Vì D, E lần lượt thuộc đường tròn đường kính BH và HC

Nên DE là tiếp tuyến của đường tròn đường kính BH
Từ chứng minh trên suy ra các phương án B, C, D đúng

Hướng dẫn:
∆
ABC ∼
∆
HBA nên 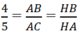
Suy ra HB = 4/5HA = 48/5 = 9,6. Chọn B.

Đáp án D
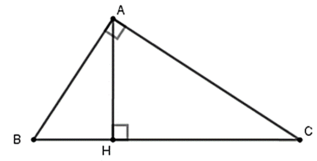
Ta có : BC = BH + HC = 9 + 16 = 25 (cm)
Áp dụng hệ thức về cạnh và đường cao trong tam giác –vuông ta có:
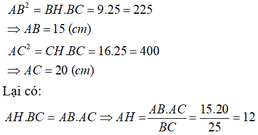

Đáp án C
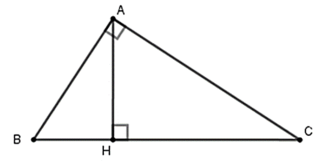
Áp dụng hệ thức về cạnh và đường cao trong tam giác vuông ta có:
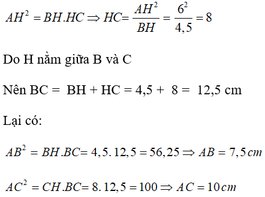

a)AB=6cm,BC=10cm
∆ABC vuông tại A đg cao AH có
#\(AC^2=BC^2-AB^2\)
AC2=100-36=64
AC=8cm
# \(AB^2=BH.BC\)
36=BH.10
BH=3,6cm
# CH=BC-BH=10-3,6=6,4cm
# \(AH^2=BH.CH\)
AH2=3,6.6,4=23,04
AH=4,8cm
b)
∆ABC vuông tại A đg cao AH có
#\(AB^2=BC^2-AC^2\)
AB2=625-400=225
AB=15cm
# \(AB^2=BH.BC\)
225=BH.25
BH=9cm
# CH= BC-BH=25-9=16cm
# \(AH.BC=AB.AC\)
AH.25=15.20=300
AH=12cm

a, Tìm được BH=9cm, CH=16cm, AB=15cm, và AC=20cm
b, Tìm được A M H ^ ≈ 73 , 74 0
c, S A H M = 21 c m 2

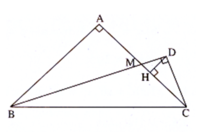
Theo câu a), từ AB = 2AM, suy ra HC = 2HD. Ta có HC < MC (h là chân đường cao hạ từ D của tam giác DCM vuông tại D) nên HC = 2HD < MC = AM < AH (do M nằm giữa A và H), vì thế 2HD không thể bằng AH. Khẳng định b) là sai.

( cot C = tan B = 4 3 vì góc B và góc C là hai góc phụ nhau)
Áp dụng hệ thức về cạnh và hình chiếu trong tam giác vuông ta có:
A B 2 = B H . B C ⇒ B H = A B 2 B C = 12 2 20 = 7,2 ( c m )