cho 2 hs (P):y=\(\dfrac{-x^2}{2}\) và (d):y=2x-6
a) Tìm tọa độ giao điểm
b) Tìm các điểm thuộc (P) có tung độ là -1
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
PD
1
AH
Akai Haruma
Giáo viên
31 tháng 3 2022
Lời giải:
a. PT hoành độ giao điểm:
$\frac{-x}{2}=2x-6$
$\Leftrightarrow x=2,4$
$y=\frac{-x}{2}=-1,2$
Vậy tọa độ giao điểm của 2 đths là $(2,4; -1,2)$
b.
$y=\frac{-x}{2}=-1$
$\Leftrightarrow x=2$
Vậy điểm có tung độ $-1$ thuộc $(P)$ là: $(2; -1)$
16 tháng 3 2022
b: Tọa độ giao điểm là:
\(\left\{{}\begin{matrix}-\dfrac{1}{4}x^2-\dfrac{1}{2}x=0\\y=\dfrac{1}{2}x\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}\dfrac{1}{2}x\left(\dfrac{1}{2}x+1\right)=0\\y=\dfrac{1}{2}x\end{matrix}\right.\Leftrightarrow\left(x,y\right)\in\left\{\left(0;0\right);\left(-2;-1\right)\right\}\)
c: Gọi M(2y;y)
Thay x=2y và y=y vào (P), ta được:
\(y=\dfrac{-1}{4}\cdot\left(2y\right)^2=\dfrac{-1}{4}\cdot4y^2=-y^2\)
=>y(y+1)=0
=>y=0 hoặc y=-1
=>x=0 hoặc x=-2
1 tháng 8 2023
a: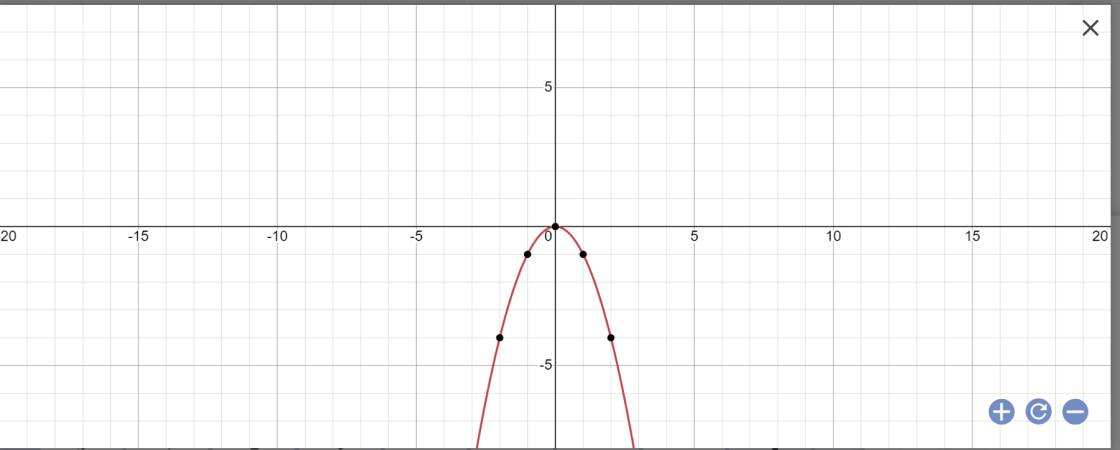 
b: PTHĐGĐ là:
-x^2=1/2x-3
=>-2x^2=x-6
=>-2x^2-x+6=0
=>2x^2+x-6=0
=>2x^2+4x-3x-6=0
=>(x+2)(2x-3)=0
=>x=3/2 hoặc x=-2
Khi x=-2 thì y=-(-2)^2=4
Khi x=3/2 thì y=-(3/2)^2=-9/4
c: Thay y=-x vào (P), ta được:
-x^2=-x
=>x^2=x
=>x(x-1)=0
=>x=0 hoặc x=1
Khi x=0 thì y=0
Khi x=1 thì y=-1
Vậy: Điểm cần tìm là M(1;-1) hoặc O(0;0)
27 tháng 1
b: Thay m=2 vào (d), ta được:
y=2x-2+1=2x-1
Phương trình hoành độ giao điểm là:
\(x^2=2x-1\)
=>\(x^2-2x+1=0\)
=>(x-1)^2=0
=>x-1=0
=>x=1
Thay x=1 vào (P), ta được:
\(y=1^2=1\)
Vậy: Khi m=2 thì (P) cắt (d) tại A(1;1)
b: Phương trình hoành độ giao điểm là:
\(x^2=2x-m+1\)
=>\(x^2-2x+m-1=0\)
\(\text{Δ}=\left(-2\right)^2-4\cdot1\cdot\left(m-1\right)\)
=4-4m+4
=-4m+8
Để (P) cắt (d) tại hai điểm phân biệt thì Δ>0
=>-4m+8>0
=>-4m>-8
=>m<2
Theo Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=2\\x_1x_2=\dfrac{c}{a}=m-1\end{matrix}\right.\)
y1,y2 thỏa mãn gì vậy bạn?
Y
15 tháng 10 2023
Bạn tự vẽ nhé.
\(a,\) 2 đồ thị hàm số \(y=2x,y=-3x+5\) giao nhau khi và chỉ khi :
\(2x=-3x+5\\ \Leftrightarrow5x=5\\ \Leftrightarrow x=1\)
Thay \(x=1\) vào \(y=2x\Leftrightarrow y=2\)
Vậy giao điểm của 2 đồ thị là \(\left(1;2\right)\)
\(b,\) 2 đồ thị hàm số \(y=3x+2,y=-\dfrac{1}{2}x+1\) giao nhau khi và chỉ khi :
\(3x+2=-\dfrac{1}{2}x+1\\ \Leftrightarrow\dfrac{7}{2}x=-1\\ \Leftrightarrow x=-\dfrac{2}{7}\)
Thay \(x=-\dfrac{2}{7}\) vào \(y=3x+2\Rightarrow y=\dfrac{8}{7}\)
Vậy giao điểm của 2 đồ thị là \(\left(-\dfrac{2}{7};\dfrac{8}{7}\right)\)
\(c,\) 2 đồ thị hàm số \(y=\dfrac{3}{2}x-2,y=-\dfrac{1}{2}x+2\) giao nhau khi và chỉ khi :
\(\dfrac{3}{2}x-2=-\dfrac{1}{2}x+2\\ \Leftrightarrow2x=4\\ \Leftrightarrow x=2\)
Thay \(x=2\) vào \(y=\dfrac{3}{2}x-2\Rightarrow y=1\)
Vậy giao điểm của 2 đồ thị là \(\left(2;1\right)\)
\(d,\) 2 đồ thị hàm số \(y=-2x+5,y=x+2\) giao nhau khi và chỉ khi :
\(-2x+5=x+2\\ \Leftrightarrow-3x=-3\\ \Leftrightarrow x=1\)
Thay \(x=1\) vào \(y=x+2\Rightarrow y=3\)
Vậy giao điểm của 2 đồ thị là \(\left(1;3\right)\)
a: PTHĐGĐ là:
-1/2x^2-2x+6=0
=>x^2+4x-12=0
=>(x+6)(x-2)=0
=>x=2 hoặc x=-6
=>y=-1/2*2^2=-2 hoặc y=-1/2*(-6)^2=-1/2*36=-18
b: y=-1
=>-1/2x^2=-1
=>x^2=2
=>x=căn 2 hoặc x=-căn 2