Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a, tự vẽ nha bạn
b1, ta có AB có hàm số y= ax+b (*) .mà nó đi qua A(-2/3 ,-7)
=> thay x=-2/3 và y= -7 vào (*) có: -7 = -2/3a +b (1)
tương tự với điểm B(-2 ,1) => 1= -2a+b (2)
từ (1) và (2) ta có hệ :\(\hept{\begin{cases}-\frac{2}{3}a+b=-7\\-2a+b=1\end{cases}}\)
giải hệ ta dc : a=... , b=... (dùng máy tính casio fx 500 hay 570 chức năng EQN )
=> AB có dạng : y = ..x + ... (ahihi lười ấn)
b2, theo câu b , AB có dạng ... xét pt hoành độ gđ của AB và parabol (p)
-2x2 = ( vế ...x +... ở trên)
giải pt bậc 2 ra hai nghiệm x1 , x2 =>hai nghiệm y1, y2 tương ứng (bằng cách thay x vào hs (p) hoặc AB tính ra y)
=> tọa độ 2 giao điểm C(x1 , y1) ,D(x2, y2)
c,( quá dễ)
ta có điểm E( xe, ye) là điểm cần tìm .
mà tổng tung và hoành độ của nó = -6
=> xe+ye = -6 (3)
mà điểm E thuộc đths (p)
=> ye = -2xe2 (4)
thay (4) vào (3) ta có pt bậc 2:
-2x2 + x = -6
giải pt ta thu đc xe=... => ye= ... ( auto lười ấn )
=> E ( ... , ... )
xooooooooooooooooooooooooooog !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
Bài giải:
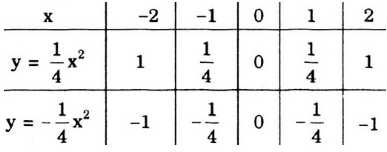
Vẽ đồ thị: y = 
x2
|
x |
-6 |
-3 |
0 |
3 |
6 |
|
y = |
12 |
3 |
0 |
3 |
12 |
y = -x + 6
- Cho x = 0 => y = 6.
- Cho y = 0 => x = 6.
Vẽ đồ thị: xem hình bên dưới.
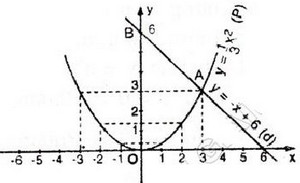
b) Giá trị gần đúng của tọa độ câc giao điểm (thực ra đây là giá trị đúng).
Hai đồ thị cắt nhau tại hai điểm A và B.
Theo đồ thị ta có A(3; 3) và B(-6; 12).
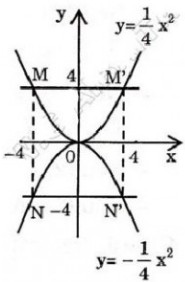
a) Đồ thị được vẽ như hình bên.
b) Vì M thuộc đồ thị y = y = 
x + 2 và tung độ của nó là y = 1 nên x + 2= 1.
Suy ra x = -1,5.
Vậy M(-1,5; 1).
Vì N thuộc đồ thị y = - 
x + 2 và tung độ của N là y = 1 nên - x + 2 = 1.
Suy ra x = .
Vậy N(; 1).
Bài giải:
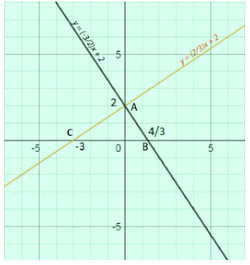
a) Đồ thị được vẽ như hình bên.
b) Vì M thuộc đồ thị y = y = x + 2 và tung độ của nó là y = 1 nên x + 2= 1.
Suy ra x = -1,5.
Vậy M(-1,5; 1).
Vì N thuộc đồ thị y = - x + 2 và tung độ của N là y = 1 nên - x + 2 = 1.
Suy ra x = .
Vậy N(; 1)