giải chi tiết nhé
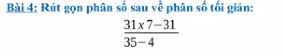
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a: Ta có: \(AB^2+CH^2\)
\(=AH^2+BH^2+AC^2-AH^2\)
\(=AC^2+BH^2\)

\(=\dfrac{16}{4}=4\) ( tính chất cơ bản của phân số )
\(=\dfrac{9}{27}=\dfrac{1}{3}\)

a: Khi m=-1/2 thì (1) sẽ là;
\(x^2-3x-\dfrac{15}{4}=0\)
=>\(x=\dfrac{3\pm2\sqrt{6}}{2}\)
b: \(\text{Δ}=\left(2m+4\right)^2-4\left(m^2-4\right)\)
\(=4m^2+16m+16-4m^2+16=16m+32\)
Để (1) có hai nghiệm pb thì 16m+32>0
=>m>-2
\(\left(x_1-x_2\right)^2=\left(x_1+x_2\right)^2-4x_1x_2\)
\(=\left(2m+4\right)^2-4\left(m^2-4\right)\)
\(=4m^2+16m+16-4m^2+16m=16m+32\)
=>x1-x2=căn 16m+32 hoặc x1-x2=-căn 16m+32
\(\dfrac{x_1}{x_2}-\dfrac{x_2}{x_1}=2\)
=>\(\dfrac{x_1^2-x_2^2}{x_1x_2}=2\)
=>\(\left(x_1-x_2\right)\cdot\dfrac{2m+4}{m^2-4}=2\)
TH1: (x1-x2)=căn 16m+32
=>\(\sqrt{16m+32}=2:\dfrac{2m+4}{m^2-4}=\dfrac{2\left(m^2-4\right)}{2\left(m+2\right)}=m-2\)
=>16m+32=m^2-4m+4 và m>=2
=>m^2-20m-28=0 và m>=2
=>\(m=10+8\sqrt{2}\)
TH2: x1-x2=-căn 16m+32
=>\(\sqrt{16m+32}=2-m\)
=>m^2-4m+4=16m+32 và m<=2
=>\(m=10-8\sqrt{2}\)

3:
Gọi độ dài CD là x
Vận tốc người 1 là x/2
Vận tốc người 2 là x/3
Theo đề, ta có: 2/3(x/2-x/3)=20
=>x/2-x/3=30
=>x/6=30
=>x=180

\(A=\dfrac{\sqrt{x}+2}{\sqrt{x}-1}=\dfrac{\sqrt{x}-1+3}{\sqrt{x}-1}=1+\dfrac{3}{\sqrt{x}-1}\)
Để \(A\in Z\Rightarrow\dfrac{3}{\sqrt{x}-1}\in Z\Rightarrow3⋮\sqrt{x}-1\Rightarrow\sqrt{x}-1\in\left\{3;1;-1;-3\right\}\)
\(\Rightarrow x\in\left\{16;4;0\right\}\)
\(B=\dfrac{2\sqrt{x}-3}{\sqrt{x}+2}=\dfrac{2\left(\sqrt{x}+2\right)-7}{\sqrt{x}+2}=2-\dfrac{7}{\sqrt{x}+2}\)
Để \(B\in Z\Rightarrow\dfrac{7}{\sqrt{x}+2}\in Z\Rightarrow7⋮\sqrt{x}+2\Rightarrow\sqrt{x}+2\in\left\{1;7;-1;-7\right\}\)
\(\Rightarrow x=25\)
Lời giải:
a.
\(A=\frac{\sqrt{x}+2}{\sqrt{x}-1}=1+\frac{3}{\sqrt{x}-1}\)
Với $x$ nguyên, để $A$ nguyên thì $\sqrt{x}-1$ phải là ước của $3$
$\Rightarrow \sqrt{x}-1\in\left\{\pm 1;\pm 3\right\}$
$\Rightarrow \sqrt{x}\in\left\{0; 2; -2; 4\right\}$
Vì $\sqrt{x}\geq 0$ nên $\sqrt{x}\in\left\{0;2;4\right\}$
$\Rightarrow x\in\left\{0;4;16\right\}$
b.
$B=\frac{2(\sqrt{x}+2)-7}{\sqrt{x}+2}=2-\frac{7}{\sqrt{x}+2}$
Để $B$ nguyên thì $\sqrt{x}+2$ là ước của $7$. Mà $\sqrt{x}+2\geq 2$ nên $\sqrt{x}+2\in\left\{7\right\}$
$\Rightarrow x=25$


CHÚC EM HỌC TỐT NHA![]()
(Chị lười kẻ bảng quá nên gạch ý như thế này, em không hiểu chỗ nào cứ cmt lại chị sẽ giải thích nha)

Bài 18
a, Với \(a>0;a\ne1;4\)
\(A=\left(\dfrac{1}{\sqrt{a}-1}-\dfrac{1}{\sqrt{a}}\right):\left(\dfrac{\sqrt{a}+1}{\sqrt{a}-2}-\dfrac{\sqrt{a}+2}{\sqrt{a}-1}\right)\)
\(=\left(\dfrac{\sqrt{a}-\sqrt{a}+1}{\sqrt{a}\left(\sqrt{a}-1\right)}\right):\left(\dfrac{a-1-a+4}{\left(\sqrt{a}-2\right)\left(\sqrt{a}-1\right)}\right)\)
\(=\dfrac{1}{\sqrt{a}\left(\sqrt{a}-1\right)}:\dfrac{3}{\left(\sqrt{a}-2\right)\left(\sqrt{a}-1\right)}=\dfrac{\sqrt{a}-2}{3\sqrt{a}}\)
b, Thay a = 9 => căn a = 3
\(A=\dfrac{3-2}{3.3}=\dfrac{1}{9}\)
c, Ta có : \(A.B=\dfrac{\sqrt{a}-2}{3\sqrt{a}}.\dfrac{3\sqrt{a}}{\sqrt{a}+1}=\dfrac{\sqrt{a}-2}{\sqrt{a}+1}< 0\)
Vì \(\sqrt{a}+1>\sqrt{a}-2\)
\(\left\{{}\begin{matrix}\sqrt{a}+1>0\\\sqrt{a}-2< 0\end{matrix}\right.\Leftrightarrow a< 4\)
Kết hợp với đk vậy \(0< a< 4;a\ne1\)
Bài 18:
1) Ta có: \(A=\left(\dfrac{1}{\sqrt{a}-1}-\dfrac{1}{\sqrt{a}}\right):\left(\dfrac{\sqrt{a}+1}{\sqrt{a}-2}-\dfrac{\sqrt{a}+2}{\sqrt{a}-1}\right)\)
\(=\dfrac{\sqrt{a}-\sqrt{a}+1}{\sqrt{a}\left(\sqrt{a}-1\right)}:\dfrac{a-1-a+4}{\left(\sqrt{a}-2\right)\left(\sqrt{a}-1\right)}\)
\(=\dfrac{1}{\sqrt{a}\left(\sqrt{a}-1\right)}\cdot\dfrac{\left(\sqrt{a}-1\right)\left(\sqrt{a}-2\right)}{3}\)
\(=\dfrac{\sqrt{a}-2}{3\sqrt{a}}\)
2) Thay a=9 vào B, ta được:
\(B=\dfrac{3\cdot3}{3+1}=\dfrac{9}{4}\)
\(=\dfrac{31\cdot\left(7-1\right)}{31}=6\)
\(\dfrac{217-31}{31}=\dfrac{186}{31}=6\)