Cho Tam giác ABC cân tại A có hai đường cao BE,CF
Chứng minh AE=AF
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
27 tháng 2 2023
Xét ΔAFC vuông tại F và ΔAEB vuông tại E có
CF=BE
góc ACF=gócABE
=>ΔAFC=ΔAEB
=>AC=AB
Xét ΔCEB vuông tại E và ΔCDA vuông tại D có
EB=DA
góc C chung
=>ΔCEB=ΔCDA
=>CB=CA=AB
=>ΔABC đều
17 tháng 8 2019
A B C E D F
Xét \(\Delta ABF\)có:
\(CD//BF\left(gt\right)\)
\(D\varepsilon AB;E\varepsilon AF\)
\(\Rightarrow\frac{AC}{AF}=\frac{AD}{AB}\)(Định lý Ta-let)
\(\Rightarrow AC.AB=AF.AD\)
mà \(AB=AC\)(vì \(\Delta ABC\)cân tại A)
\(\Rightarrow AC^2=AF.AD\)(1)
Vì \(BE\perp AC\)(gt) \(\Rightarrow\Delta AEB\)vuông tại E
Vì \(CD\perp AB\)(gt) \(\Rightarrow\Delta ACD\)vuông tại D
Xét \(\Delta AEB\)vuông tại E và \(\Delta ACD\)vuông tại D có
\(\widehat{BAC}\)chung
\(AB=AC\)(cmt)
\(\Rightarrow\Delta AEB=\Delta ADB\)(TH: cạnh huyền,góc nhọn)
\(\Rightarrow AE=AD\)(2 cạnh tương ứng) (2)
Từ (1) và (2) đpcm
Đây là cách giải của mình ạ
CM
15 tháng 1 2019
Ta có: ΔABC cân tại A
⇒ AE là đường cao đồng thời là đường phân giác ∠BAC.
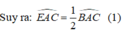
+) Tam giác ABC cân tại A nên AB = AC.
Lại có: AD = AB( giả thiết)
Suy ra: AD = AC
Do đó: ΔADC cân tại A
+) Trong tam giác ADC có: AF là đường caon nên đồng thời là đường phân giác ∠CAD.
25 tháng 6 2023
a: Xét ΔABE vuông tại E và ΔACF vuông tại F có
góc A chung
=>ΔABE đồng dạng với ΔACF
b: ΔABE đồng dạng với ΔACF
=>AE/AF=AB/AC
=>AE/AB=AF/AC và AE*AC=AB*AF
Xét ΔAEF và ΔABC có
AE/AB=AF/AC
góc FAE chung
=>ΔAEF đồng dạng với ΔABC
TM
30 tháng 9 2017
hình tự vẽ
a)\(\Delta ABE=\Delta ACF\)(ch-gn) do: \(\widehat{AEB}=\widehat{AFC}=90^o\);\(\widehat{BAC}\) chung;AB=AC(do \(\Delta ABC\)cân tại A)
=>AE=AF(2 cạnh tương ứng)
b) AE=AF=>\(\Delta EAF\) cân tại A=>\(\widehat{AFE}=\widehat{AEF}=\frac{180^o-\widehat{EAF}}{2}\)(1)
tam giác ABC cân tại A => \(\widehat{ABC}=\widehat{ACB}=\frac{180^o-\widehat{BAC}}{2}\)(2)
Từ (1) và (2) => \(\widehat{AFE}=\widehat{AEF}=\)\(\widehat{ABC}=\widehat{ACB}\)
trong đó \(\widehat{AFE}\) đồng vị với \(\widehat{ABC}\) và \(\widehat{AEF}\)đồng vị với \(\widehat{ACB}\)
=> EF//BC => BCEF là hình thang
hình thang BCEF có: \(\widehat{ABC}=\widehat{ACB}\) hay \(\widehat{FBC}=\widehat{ECB}\) => hình thang BCEF cân
A B C F E
Kẻ EF // BC
Xét \(\Delta AEF\)có:
Góc C = Góc E
Góc F = Góc B ( EF // BC; 2 góc đồng vị)
\(\Rightarrow\Delta AEF\)cân tại A.
nên AE = AF
Xét \(\Delta ACF\)và \(\Delta ABE\)
Góc A chung (gt)
AC = AB (gt)
\(\Rightarrow\Delta ACF=\Delta ABE\)(cạnh huyền- góc nhọn)
\(\Rightarrow AF=AE\)