mng giúp em c4 với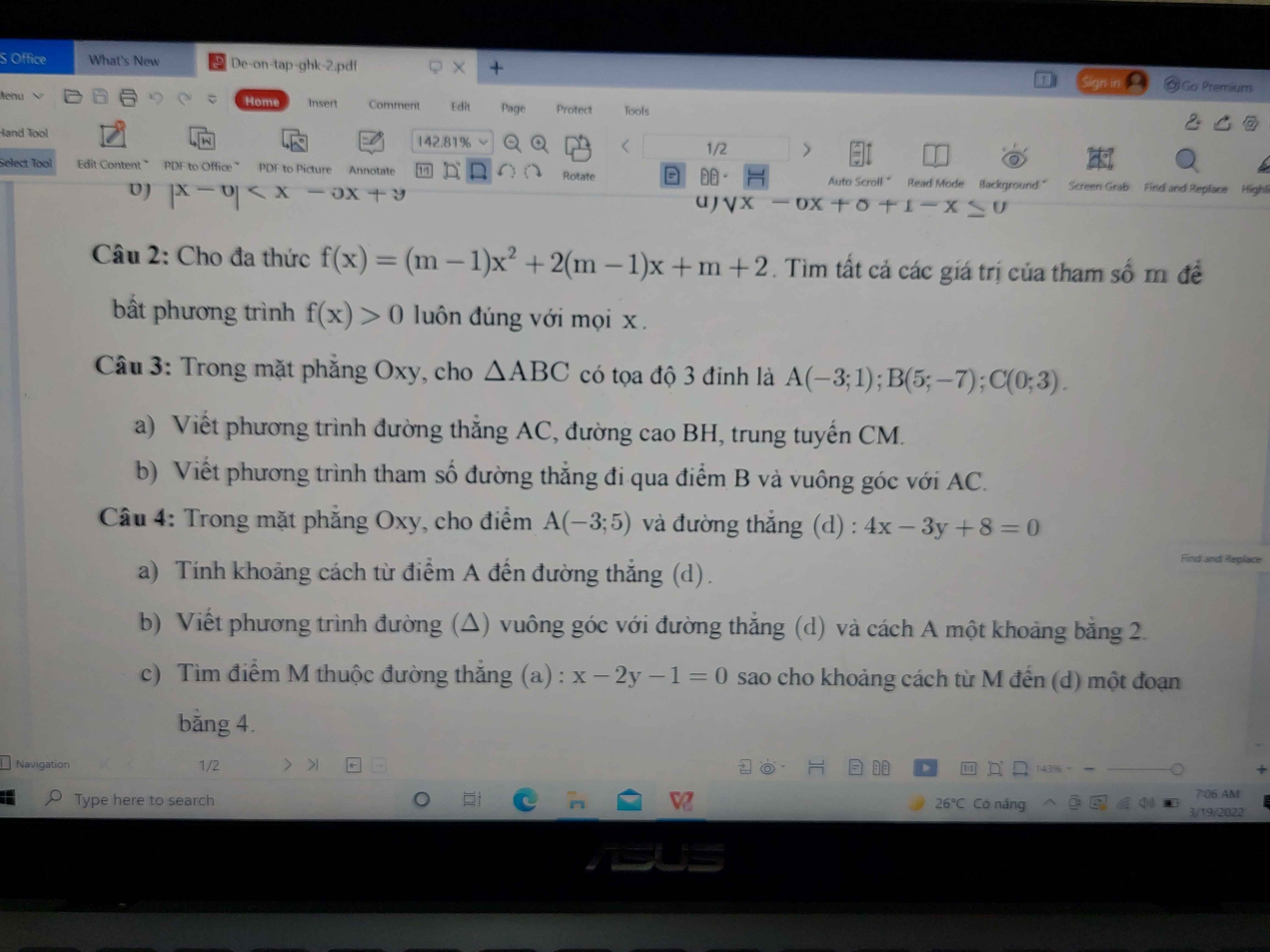
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
MNG GIÚP EM BÀI 2 VỚI Ạ EM CẢM ƠN MNG NHIỀU Ạ
11 tháng 4 2022
Bài 2:
a: \(f\left(x\right)=-9x^3-2x^2+6x-3\)
\(G\left(x\right)=9x^3-6x+53\)
b: \(H\left(x\right)=9x^3-6x+53-9x^3-2x^2+6x-3=-2x^2+50\)
c: Đặt H(x)=0
=>2x2-50=0
=>x=5 hoặc x=-5
CD
1
10 tháng 5 2021
Câu 2:
uses crt;
var a:array[1..100]of integer;
i,n,t:integer;
begin
clrscr;
write('Nhap n='); readln(n);
for i:=1 to n do
begin
write('A[',i,']='); readln(a[i]);
end;
t:=0;
for i:=1 to n do
if (4<a[i]) and (a[i]<15) then t:=t+a[i];
writeln(t);
readln;
end.
3 tháng 8 2023
1. should ask
*must not ask là sai vì người quản lí mới nên hỏi vài câu hỏi trước khi thực hiện thay đổi
*have to ask (mang tính chủ quan) nên có làm hay không làm cũng được nên ta không chọn đáp án này
2. could prevent
Vì sau would, could là V_inf
4 tháng 12 2023
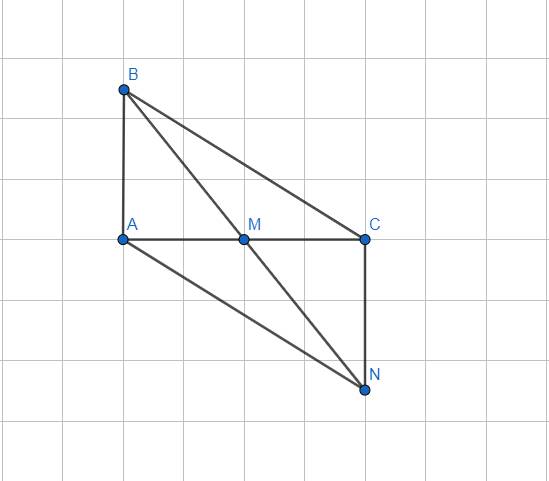
Xét ΔMAB và ΔMCN có
MA=MC
\(\widehat{AMB}=\widehat{CMN}\)
MB=MN
Do đó: ΔMAB=ΔMCN
=>AB=CN và \(\widehat{MAB}=\widehat{MCN}=90^0\)
=>CN\(\perp\)AC
Xét ΔMAN và ΔMCB có
MA=MC
\(\widehat{AMN}=\widehat{CMB}\)(hai góc đối đỉnh)
MN=MB
Do đó: ΔMAN=ΔMCB
=>AN=CB
ΔMAN=ΔMCB
=>\(\widehat{MAN}=\widehat{MCB}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AN//CB
HP
8 tháng 4 2021
1.
\(1+tan\alpha+tan^2\alpha+tan^3\alpha\)
\(=1+\dfrac{sin\alpha}{cos\alpha}+\dfrac{sin^2\alpha}{cos^2\alpha}+\dfrac{sin^3\alpha}{cos^3\alpha}\)
\(=1+\dfrac{sin\alpha}{cos\alpha}+\dfrac{sin^2\alpha}{cos^2\alpha}\left(1+\dfrac{sin\alpha}{cos\alpha}\right)\)
\(=\left(\dfrac{sin^2\alpha}{cos^2\alpha}+1\right)\left(1+\dfrac{sin\alpha}{cos\alpha}\right)\)
\(=\dfrac{1}{cos^2\alpha}\left(1+\dfrac{sin\alpha}{cos\alpha}\right)=\dfrac{sin\alpha+cos\alpha}{cos^3\alpha}\)
giúp em với mng!!!
10 tháng 11 2021
\(c,A\left(-2;2\right)\inđths\Leftrightarrow-2a+b=2\left(1\right)\\ Đths//Ox\Leftrightarrow a=0;b=y\left(2\right)\\ \left(1\right)\left(2\right)\Leftrightarrow a=0;b=2\)
a.
\(d\left(A;d\right)=\dfrac{\left|4.\left(-3\right)-3.5+8\right|}{\sqrt{4^2+\left(-3\right)^2}}=-\dfrac{19}{5}\)
b.
Do \(\Delta\perp d\) nên \(\Delta\) nhận (3;4) là 1 vtpt
Phương trình \(\Delta\) có dạng: \(3x+4y+c=0\)
\(d\left(A;\Delta\right)=2\Leftrightarrow\dfrac{\left|-3.3+4.5+c\right|}{\sqrt{3^2+4^2}}=2\)
\(\Leftrightarrow\left|c+11\right|=10\Rightarrow\left[{}\begin{matrix}c=-21\\c=-1\end{matrix}\right.\)
Có 2 đường thẳng thỏa mãn: \(\left[{}\begin{matrix}3x+4y-1=0\\3x+4y-21=0\end{matrix}\right.\)
c.
Do \(M\in\left(a\right)\) nên tọa độ có dạng: \(M\left(2m+1;m\right)\)
\(d\left(M;d\right)=\dfrac{\left|4\left(2m+1\right)-3m+8\right|}{\sqrt{4^2+\left(-3\right)^2}}=4\)
\(\Leftrightarrow\left|5m+12\right|=20\Rightarrow\left[{}\begin{matrix}m=\dfrac{8}{5}\\m=-\dfrac{32}{5}\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}M\left(\dfrac{21}{5};\dfrac{8}{5}\right)\\M\left(-\dfrac{59}{5};-\dfrac{32}{5}\right)\end{matrix}\right.\)