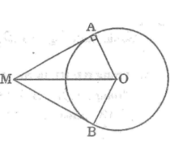
2 tiếp tuyến tại A và B của đường tròn (O) cắt nhau tại M ,biết AOB = 100° ,tính MAB
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Những câu hỏi liên quan

20 tháng 1
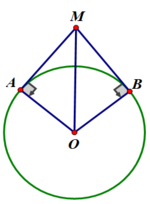
Xét tứ giác OAMB có
\(\widehat{OAM}+\widehat{OBM}+\widehat{AOB}+\widehat{AMB}=360^0\)
=>\(\widehat{AMB}+100^0+90^0+90^0=360^0\)
=>\(\widehat{AMB}=80^0\)

18 tháng 5 2022
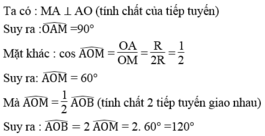
Xét ΔAOM vuông tại A có \(\cos\widehat{OAM}=\dfrac{R}{2R}=\dfrac{1}{2}\)
nên \(\widehat{OAM}=60^0\)(1)
Xét (O) có
MA là tiếp tuyến
MB là tiếp tuyến
Do đó: OM là phân giác của góc AOB(2)
Từ (1) và (2) suy ra \(\widehat{AOB}=120^0\)
PL
0

Yêu cầu của bạn có phải tính góc MAB không?
Nếu có thì sau đây là bài giải!
Giải:
Góc AOM=50o, góc AMO=40o (tam giác AOM vuông tại A).
AB vuông góc với OM (AM và BM là hai tiếp tuyến của (O,OA).
Suy ra, góc MAB+góc AMO=90o \(\Leftrightarrow\) Góc MAB=90o-góc AMO=90o-40o=50o.