Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Mình làm tắt nha bạn không hiểu đâu thì hỏi lại nhé
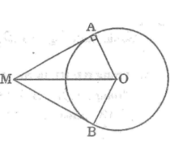
a) MA, MB là tiếp tuyến
=> \(\widehat{OBM}=\widehat{OAM}=90^o\) (t/c tiếp tuyến)
=> \(\widehat{OBM}+\widehat{OAM}=180^o\)
mà 2 góc đối nhau
=> tứ giác AOBM nội tiếp
=> 4 điểm A, O, B, M cùng thuộc 1 đường tròn
b) Áp dụng hệ thức lượng vào tam giác OAM vuông tại A đường cao AH
=> \(AM^2=MH.MO\)
Áp dụng hệ thức lượng vào tam giác DAM vuông tại A đường cao AC
=> \(AM^2=MC.MD\)
=> \(AM^2=MH.MO=MC.MD\)

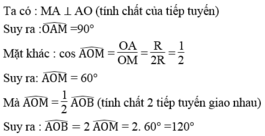
Xét ΔAOM vuông tại A có \(\cos\widehat{OAM}=\dfrac{R}{2R}=\dfrac{1}{2}\)
nên \(\widehat{OAM}=60^0\)(1)
Xét (O) có
MA là tiếp tuyến
MB là tiếp tuyến
Do đó: OM là phân giác của góc AOB(2)
Từ (1) và (2) suy ra \(\widehat{AOB}=120^0\)

a: góc OAM+góc OBM=90+90=180 độ
=>AOBM nội tiếp
b: góc BOM=1/2*góc AOB=góc BCA
a giải thích em làm sao 1/2 AOB = góc BCA được ạ
Đáp án là C
Xét tam giác MAO vuông tại A có AO = R; MA = R 3