Cho đường thẳng \(mx+\left(2-3m\right)y+m-1=0\left(d\right)\) Điểm cố định mà đường thẳng (d) luôn đi qua với mọi ...
Đọc tiếp
Cho đường thẳng \(mx+\left(2-3m\right)y+m-1=0\left(d\right)\) Điểm cố định mà đường thẳng (d) luôn đi qua với mọi là:
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
KN
16 tháng 4 2020
Điều kiện cần và đủ để đường thẳng \(\left(m-2\right)x+\left(m-1\right)y=1\) đi qua điểm cố định \(N\left(x_0;y_0\right)\)với mọi m là:
\(\left(m-2\right)x_0+\left(m-1\right)y_0=1\forall m\)
\(\Leftrightarrow mx_0-2x_0+my_0-y_0-1=0\forall m\)
\(\Leftrightarrow\left(x_0+y_0\right)m-\left(2x_0+y_0+1\right)=0\forall m\)
\(\Leftrightarrow\hept{\begin{cases}x_0+y_0=0\\2x_0+y_0+1=0\end{cases}\Leftrightarrow}\hept{\begin{cases}x_0=-1\\y_0=1\end{cases}}\)
Vậy các đường thẳng \(\left(m-2\right)x+\left(m-1\right)y=1\) luôn đi qua điểm cố định N(-1; 1)
NV
Nguyễn Việt Lâm
Giáo viên
15 tháng 12 2020
a.
Giả sử điểm cố định mà (d) đi qua có tọa độ \(M\left(x_0;y_0\right)\)
Với mọi m, ta có:
\(y_0=\left(m+2\right)x_0+m\)
\(\Leftrightarrow m\left(x_0+1\right)+2x_0-y_0=0\)
\(\Leftrightarrow\left\{{}\begin{matrix}x_0+1=0\\2x_0-y_0=0\end{matrix}\right.\) \(\Rightarrow M\left(-1;-2\right)\)
b. Để (d) cắt 2 trục tạo thành tam giác thì \(m\ne\left\{0;-2\right\}\)
Khi đó ta có: \(\left\{{}\begin{matrix}A\left(-\dfrac{m}{m+2};0\right)\\B\left(0;m\right)\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}OA=\left|\dfrac{m}{m+2}\right|\\OB=\left|m\right|\end{matrix}\right.\)
\(S_{OAB}=\dfrac{1}{2}OA.OB=\dfrac{1}{2}\)
\(\Leftrightarrow\dfrac{m^2}{\left|m+2\right|}=1\)
\(\Leftrightarrow\left[{}\begin{matrix}m^2=m+2\\m^2=-m-2\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}m=-1\\m=2\end{matrix}\right.\)
VB
Cho đường thẳng d: y = (3m 2 +1)x + m 2 - 4. Tìm điểm cố định mà đường thẳng d luôn đi qua với mọi m
0
VT
7 tháng 10 2018
TH1: m = 0 => -2y = 2 => y = -1
Nên (d) đi qua điểm (0; -1) cố định
TH2: m # 0
Giả sử A(xo;yo) là điểm mà (d) luôn đi qua
\(\Leftrightarrow m\sqrt{3}x_0+2my_0-2y_0-m-2=0\\ \Leftrightarrow m\left(\sqrt{3}x_0+2y_0-1\right)-2y_0-2=0\\ \Leftrightarrow\left\{{}\begin{matrix}\sqrt{3}x_0+2y_0-1=0\\2y_0+2=0\end{matrix}\right.\\ \Leftrightarrow\left\{{}\begin{matrix}y_0=-1\\x=\sqrt{3}\end{matrix}\right.\)
Nên (d) đi qua điểm A(√3; -1) cố định
Vậy với mọi m, đường thẳng (d) luôn đi qua 1 điểm cố định
AH
Akai Haruma
Giáo viên
12 tháng 6 2020
Lời giải:
a)
Gọi $(x_0, y_0)$ là điểm cố định mà $(d_1)$ với mọi $m$
Khi đó:
$mx_0+(m-2)y_0+m+2=0$ với mọi $m$
$\Leftrightarrow m(x_0+y_0+1)+(2-2y_0)=0$ với mọi $m$
\(\Rightarrow \left\{\begin{matrix} x_0+y_0+1=0\\ 2-2y_0=0\end{matrix}\right.\Leftrightarrow \left\{\begin{matrix} y_0=1\\ x_0=-2\end{matrix}\right.\)
Vậy điểm cố định mà $(d_1)$ luôn đi qua với mọi $m$ là $(-2,1)$
-----------------
Gọi điểm cố định mà $(d_2)$ luôn đi qua với mọi $m$ là $(x_0,y_0)$
Ta có:
$(2-m)x_0+my_0-m-2=0$ với mọi $m$
$\Leftrightarrow m(y_0-x_0-1)+(2x_0-2)=0$ với mọi $m$
\(\Rightarrow \left\{\begin{matrix} y_0-x_0-1=0\\ 2x_0-2=0\end{matrix}\right.\Rightarrow \left\{\begin{matrix} x_0=1\\ y_0=2\end{matrix}\right.\)
Vậy điểm cố định cần tìm là $(1,2)$
b) Gọi $I(a,b)$ là giao điểm của $(d_1); (d_2)$
Ta có:
$ma+(m-2)b+m+2=0(1)$
$(2-m)a+mb-m-2=0(2)$
Lấy $(1)+(2)\Rightarrow a+(m-1)b=0$
Lấy $(1)-(2)\Rightarrow (m-1)a-b+m+2=0$
Từ 2 PT trên ta dễ dàng suy ra $b=\frac{m+2}{(m-1)^2+1}; a=\frac{(m+2)(1-m)}{(m-1)^2+1}$
Bằng khai triển ta thấy:
\((\frac{(m+2)(1-m)}{(m-1)^2+1}+\frac{1}{2})^2+(\frac{m+2}{(m-1)^2+1}-\frac{3}{2})^2=\frac{5}{2}\) là hằng số
Do đó điểm $I$ luôn thuộc đường tròn tâm $(\frac{-1}{2}; \frac{3}{2})$ bán kính $\sqrt{\frac{5}{2}}$ là đường tròn cố định.
CM
4 tháng 10 2019
Giả sử ( x 0 ; y 0 ) là điểm cố định mà đường thẳng mx + 3 + (3m – 1)y = 0 luôn đi qua.
Ta có:
m x 0 + 3 + (3m - 1) y 0 = 0 với mọi m
⇔ m x 0 + 3 + 3m y 0 - y 0 = 0 với mọi m
⇔ m( x 0 + 3 y 0 ) + 3 - y 0 = 0 với mọi m
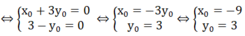
Vậy điểm cố định mà đường thẳng luôn đi qua là (-9: 3)
13 tháng 11 2023
a:
Sửa đề: \(I\left(\dfrac{1}{2};-3\right)\)
Thay \(x=\dfrac{1}{2};y=-3\) vào (d): \(y=\left(1-2m\right)x+m-\dfrac{7}{2}\), ta được:
\(\left(1-2m\right)\cdot\dfrac{1}{2}+m-\dfrac{7}{2}=-3\)
=>\(\dfrac{1}{2}-m+m-\dfrac{7}{2}=-3\)
=>\(\dfrac{1}{2}-\dfrac{7}{2}=-3\)
=>-3=-3(đúng)
vậy: I(1/2;-3) là điểm cố định mà (d): \(y=\left(1-2m\right)x+m-\dfrac{7}{2}\) luôn đi qua
b: \(\left(d\right):y=\left(2m+1\right)x+m-2\)
\(=2mx+x+m-2\)
\(=m\left(2x+1\right)+x-2\)
Điểm mà (d) luôn đi qua có tọa độ là:
\(\left\{{}\begin{matrix}2x+1=0\\y=x-2\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}x=-\dfrac{1}{2}\\y=-\dfrac{1}{2}-2=-\dfrac{5}{2}\end{matrix}\right.\)
9 tháng 5 2021
Câu 1:Đường thẳng (d):y=mx+m-1 (m≠0)(m≠0)luôn đi qua điểm cố định E khi m thay đổi.Tọa độ của điểm E là:
A.(1;1) B.(1;-1) C.(-1;-1) D.(-1;1)
Câu 2:Phương trình x2+x+m=0x2+x+m=0 có 2 nghiệm phân biệt khi:
A.m<14m<14 B.m<1 C.m>14m>14 D.m>1
Câu 3:Cho đường thẳng (d):y=ax+2.Biết rằng điểm E(1;1) thuộc đường thẳng (d).Hệ số góc của đường thẳng (d) là
A.1 B.-1 C.2 D.3
Giả sử điểm cố định mà \(\left(d\right)\)luôn đi qua là \(M\left(x_0,y_0\right)\).
Khi đó:
\(mx_0+\left(2-3m\right)y_0+m-1=0\)đúng với mọi \(m\)
\(\Leftrightarrow m\left(x_0-3y_0+1\right)+2y_0-1=0\)đúng với mọi \(m\)
\(\Leftrightarrow\hept{\begin{cases}x_0-3y_0+1=0\\2y_0-1=0\end{cases}}\Leftrightarrow x_0=y_0=\frac{1}{2}\).
Vậy điểm cố định mà \(\left(d\right)\)luôn đi qua là \(M\left(\frac{1}{2},\frac{1}{2}\right)\).