tính BC 35;70;770
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
ML
1
DH
11 tháng 3 2016
Nếu AM là đg phân giác , đg trung tuyến thì tam giác ABC vuông tại A
→AM là đg cao ,đg trung trực
BC2= AB2 + AC2
QE
2
NV
Nguyễn Việt Lâm
Giáo viên
27 tháng 7 2021
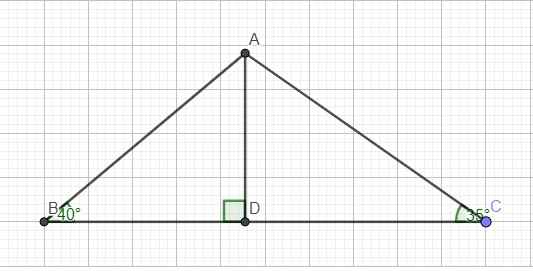
Kẻ đường cao AD ứng với BC
Trong tam giác vuông ABD:
\(cotB=\dfrac{BD}{AD}\Rightarrow BD=AD.cotB\)
Trong tam giác vuông ACD:
\(cotC=\dfrac{CD}{AD}\Rightarrow CD=AD.cotC\)
\(\Rightarrow BD+CD=AD.cotB+AD.cotC\)
\(\Rightarrow BC=AD\left(cotB+cotC\right)\)
\(\Rightarrow AD=\dfrac{BC}{cotB+cotC}\)
Trong tam giác vuông ACD:
\(sinC=\dfrac{AD}{AC}\Rightarrow AC=\dfrac{AD}{sinC}=\dfrac{BC}{sinC\left(cotB+cotC\right)}=\dfrac{20}{sin35^0\left(cot40^0+cot35^0\right)}=13,3\left(cm\right)\)
23 tháng 2 2022
a) Có : \(\widehat{A}+\widehat{B}+\widehat{C}=180^o\)( tổng số đo 3 góc trong 1 tam giác)
\(55^o+35^o+\widehat{C}=180^o\)
\(\widehat{C}=180^o-90^o\)
\(\widehat{C}=90^o\)
b) Xét \(\Delta ABC\) vuông tại C có :
\(CB^2+AC^2=AB^2\) (định lý pi-ta-go)
\(49+AC^2=100\)
\(CA^2=51\)
\(CA=\sqrt{51}\approx7.14\)
23 tháng 2 2022
a, Ta có : ^A + ^B = 900
Vậy ^C = 900
b, Vì ^C = 900
Vậy tam giác ABC vuông tại C
\(AC=\sqrt{AB^2-BC^2}=\sqrt{51}cm\)
NT
0
LN
1
DK
1
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 1 2022
\(\left(\overrightarrow{BA},\overrightarrow{BC}\right)=\widehat{ABC}=90^0-ACB=90^0-35^0=55^0\)
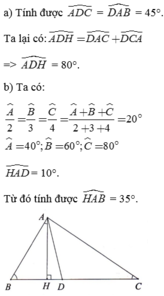
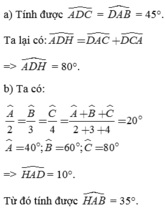
Phân tích thành tích các thừa số nguyên tố: \(35=5.7,70=2.5.7,770=2.5.7.11\)
Suy ra \(BCNN\left(35,70,770\right)=2.5.7.11=770\)
\(BC\left(35,70,770\right)=B\left(770\right)\).