Cho tam giác ABC có Góc B = Góc C = 40 độ . Vẽ BD la tia phân giác góc B. Cm BD + DA = BC
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



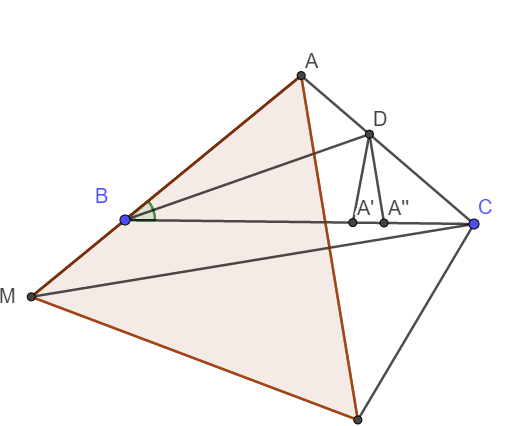
a) Trên BC lấy điểm A' và A'' sao cho BA' = BA; BA'' = BD
Do BD là phân giác góc ABA' nên ta có ngay \(\Delta ABD=\Delta A'BD\left(c-g-c\right)\)
\(\Rightarrow AD=A'D\) ; \(\widehat{BA'D}=\widehat{BAD}=180^o-40^o.2=100^o\)
\(\Rightarrow\widehat{DA'A''}=80^o\)
Xét tam giác cân BDA'' có: \(\widehat{DBA''}=20^o\Rightarrow\widehat{BA''D}=\frac{180^o-20^o}{2}=80^o\)
Suy ra DA' = DA'' và \(\widehat{A''DC}=\widehat{DA''A'}-\widehat{ACB}=40^o\)
Nên DA'' = CA''
Tóm lại thì AD = DA' = DA'' = A''C nên BC = BA''+ A''C = BD + AD
b) Vẽ tam giác đều AMF.
Ta có ngay \(\widehat{MAF}=60^o\Rightarrow\widehat{CAF}=100^o-60^o=40^o\)
Suy ra \(\Delta ABC=\Delta CAF\left(c-g-c\right)\)
\(\Rightarrow AC=CF\)
Từ đó ta có \(\Delta AMC=\Delta FMC\left(c-c-c\right)\)
\(\Rightarrow\widehat{AMC}=\widehat{FMC}\) hay MA là phân giác óc AMF.
Vậy nên \(\widehat{MAC}=30^o\)

sai ở đâu vậy ạ bạn cho mình xin ý kiến . Cảm ơn !
mình không biết mình có ns sai hay đúng nhưng nếu vẽ hình thì BC không bằng BD . Mong bạn giúp

 ∆ABC có:
∆ABC có:
∠A + ∠ABC + ∠C = 180⁰ (tổng ba góc trong ∆ABC)
⇒ ∠A = 180⁰ - ∠C - ∠ABC
= 180⁰ - 40⁰ - 80⁰
= 60⁰
Do BD là tia phân giác của ∠ABC
⇒ ∠ABD = ∠ABC : 2 = 80⁰ : 2 = 40⁰
∆ABD có:
∠A + ∠ABD + ∠ADB = 180⁰ (tổng ba góc trong ∆ABD)
⇒ ∠ADB = 180⁰ - ∠A - ∠ABD
= 180⁰ - 60⁰ - 40⁰
= 80⁰
Ta có:
∠ADB + ∠BDC = 180⁰ (kề bù)
⇒ ∠BDC = 180⁰ - ∠ADB
= 180⁰ - 80⁰
= 100⁰

a) Xét tam giác ABC vuông tại A có:
* \(BC^2=AB^2+AC^2\)(định lý Py-ta-go)
\(< =>10^2=6^2+AC^2\)
\(< =>AC^2=100-36\)
\(< =>AC=\sqrt{64}\)
\(< =>AC=8\)
Chu vi tam giác ABC là : \(AB+AC+BC=6+10+8=24\left(cm\right)\)
Diện tích tam giác ABC là: \(\frac{AB.AC}{2}=\frac{6.8}{2}=24\left(cm^2\right)\)
b) Ta có: BD là phân giác của góc B (gt)
=> \(\frac{DA}{DC}=\frac{BA}{BC}\)(tính chất đường phân giác trong 1 tam giác)
Mà \(\frac{BA}{BC}=\frac{6}{10}=\frac{3}{5}\)
=>\(\frac{DA}{DC}=\frac{3}{5}\)
c) Xét tam giác ABI có:
* BD là phân giác góc B (gt)
* BD là đường cao (AI vuông góc BD)
=> Tam gi1c ABI cân tại B
=> BA = BI (tính chất)
Xét tam giác ABD và tam giác IBD có:
*AB = IB (cmt)
*Góc ABD = Góc IBD (BD là phân giác)
*BD là cạnh chung
=> tam giác ABD = tam giác IBD (c-g-c)
=> Góc BAD = Góc BID (tính chất)
Mà góc BAD = 90 độ (tam giác ABC vuông tại A)
=> Góc BID = 90 độ

A) Xét tam giác ABD và tam giác EBD có
BD ( cạnh chung )
\(\widehat{CBD}\)= \(\widehat{ABD}\)( giả thiết )
\(\Rightarrow\)tam giác ABD = tam giác EBD ( cạnh huyền - góc nhọn )
\(\Rightarrow\)DA=DE ( hai cạnh tương ứng )
b) mà theo phần a ta lại có : \(\widehat{EDB}\)=\(\widehat{EDB}\)( hai góc tương ứng )
mà \(\widehat{ADF}\)=\(\widehat{EDC}\)( hai góc đối đỉnh )
\(\Rightarrow\)\(\widehat{CDB}\)=\(\widehat{FDB}\)( Theo hai cm trên )
BD ( cạnh chung )
\(\widehat{EBD}\)=\(\widehat{ABD}\)( giả thiết )
vậy suy ra tam giác BDF = tam giác BDC ( G-C-G)
C) Theo phần a ta có AD =ED
B ta lại có :FD = DC
suy ra tứ giác AECF là hình thang cân
suy ra AE song song FC

a: Xét ΔBAD và ΔBED có
BA=BE
góc ABD=góc EBD
BD chung
=>ΔBAD=ΔBED
=>DA=DE
b: BA=BE
DA=DE
=>BD là trung trực của AE
=>BD vuông góc AE
c: góc EDC+góc C=90 độ
góc ABC+góc C=90 độ
=>góc EDC=góc ABC