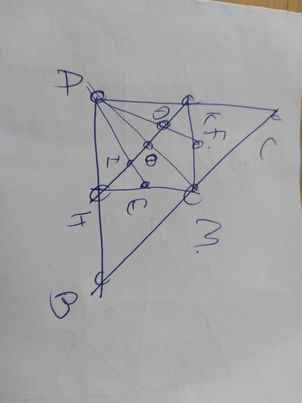
Cho Δ ABC cân tại A có AB=AC=15cm, đường trung tuyến AM=12cm.vẽ MH vuông góc AC(H ϵ AC).gọi E là trung điểm cuả BM và F là trung điểm của MH
a) Tính BC
b) Chứng minh ΔABM≈ ΔAMH
c) Chứng minh AB. AF= AE. AM
d) Chứng minh BH vuông góc AF
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
14 tháng 4 2021
a) Sửa đề: Cm AG vuông góc với BC
Ta có: \(AN=NB=\dfrac{AB}{2}\)(N là trung điểm của AB)
\(AM=MC=\dfrac{AC}{2}\)(M là trung điểm của AC)
mà AB=AC(ΔABC cân tại A)
nên AN=NB=AM=MC
Xét ΔNBC và ΔMCB có
NB=MC(cmt)
\(\widehat{NBC}=\widehat{MCB}\)(hai góc ở đáy của ΔABC cân tại A)
BC chung
Do đó: ΔNBC=ΔMCB(c-g-c)
Suy ra: \(\widehat{NCB}=\widehat{MBC}\)(hai góc tương ứng)
hay \(\widehat{GBC}=\widehat{GCB}\)
Xét ΔGBC có \(\widehat{GBC}=\widehat{GCB}\)(cmt)
nên ΔGBC cân tại G(Định lí đảo của tam giác cân)
Suy ra: GB=GC(hai cạnh bên)
Ta có: AB=AC(ΔABC cân tại A)
nên A nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(1)
Ta có: GB=GC(cmt)
nên G nằm trên đường trung trực của BC(Tính chất đường trung trực của một đoạn thẳng)(2)
Từ (1) và (2) suy ra AG là đường trung trực của BC
hay AG\(\perp\)BC(đpcm)
H
23 tháng 12 2020
Bn tự vẽ hình nha
a, Xét tứ giác HMKA có
góc MHA= 90 độ( mh ⊥ AB-gt)
góc MKA = 90 độ( MK⊥ AC - gt)
góc HAK = 90 độ( tam giác ABC ⊥ A-gt)
-> HMKA là hình chữ nhật ( tứ giác có 3 góc vuông)
-> HM song song AK; Hk=MA; HA=MK
ta có
HM song song ak(cmt)
M là trung điểm BC(gt)
-> H là trung điểm BA
-> Bh=HA=1/2 BA
mà HA=MK(cmt)
->BH=MK(1)
Xét tam giác ABC vuông tại A có
AM là đg trung tuyến(gt)
-> AM=MB=MC
mà MA=HK(cmt)
-> HK=BM(2)
Từ (1) và (2)
-> BMKH là hình bình hành( các cạnh đối bằng nhau là hình bình hành)
Sorry nhe mình ko bít lm câu C
Nếu hai câu trên đúng like cho mình nha >_<
16 tháng 12 2023
a: Xét tứ giác AHMK có
\(\widehat{AHM}=\widehat{AKM}=\widehat{HAK}=90^0\)
=>AHMK là hình chữ nhật
=>AM=HK
b: Xét ΔABC có
M là trung điểm của BC
MK//AB
Do đó: K là trung điểm của AC
Xét ΔABC có
M là trung điểm của BC
MH//AC
Do đó: H là trung điểm của AB
Xét ΔABC có
M,K lần lượt là trung điểm của CB,CA
=>MK là đường trung bình của ΔABC
=>MK//AB và \(MK=\dfrac{AB}{2}\)
Ta có: MK//AB
H\(\in\)AB
Do đó: MK//HB
Ta có: \(MK=\dfrac{AB}{2}\)
\(AH=HB=\dfrac{AB}{2}\)
Do đó: MK=AH=HB
Xét tứ giác BHKM có
BH//KM
BH=KM
Do đó: BHKM là hình bình hành
c: Gọi O là giao điểm của AM và KH
Ta có: AHMK là hình chữ nhật
=>AM cắt KH tại trung điểm của mỗi đường
=>O là trung điểm của AM và KH
=>\(OA=OM=\dfrac{AM}{2};OK=OH=\dfrac{KH}{2}\)
mà AM=KH
nên OA=OM=OK=OH(1)
Xét ΔAKM có
AF,KO là các đường trung tuyến
AF cắt KO tại D
Do đó: D là trọng tâm của ΔAKM
Xét ΔAKM có
D là trọng tâm
KO là đường trung tuyến
Do đó: \(KD=\dfrac{2}{3}KO\left(2\right)\)
Xét ΔHAM có
AE,HO là các đường trung tuyến
AE cắt HO tại I
Do đó: I là trọng tâm của ΔHAM
Xét ΔHAM có
HO là đường trung tuyến
I là trọng tâm
Do đó: \(HI=\dfrac{2}{3}HO\left(3\right)\)
Từ (1),(2),(3) suy ra HI=KD
22 tháng 2 2022
a: Ta có: ΔABC cân tại A
mà AM là đường trung tuyến
nên AM là đường cao
b: Ta có: ΔABC cân tại A
mà AM là đường cao
nên AM là tia phân giác của góc BAC
hay góc BAM= góc CAM
c: Xét ΔAHM vuông tại H và ΔAKM vuông tại K có
AM chung
\(\widehat{HAM}=\widehat{KAM}\)
Do đó: ΔAHM=ΔAKM
Suy ra: MH=MK
hay ΔMHK cân tại M
d: Xét ΔAHK có AH=AK
nên ΔAHK cân tại A
e: Xét ΔABC có AH/AB=AK/AC
nên HK//BC
a) Ta có \(BC=2BM=2\sqrt{AB^2-AM^2}=2.\sqrt{9}=6\).
b) Xét \(\Delta ABM\) và \(\Delta AMH\) có \(\widehat{AMB}=\widehat{AHM}=90^o;\widehat{BAM}=\widehat{MAH}\)
\(\Rightarrow\Delta ABM\sim\Delta AMH\left(g.g\right)\).
c) \(\Delta ABM\sim\Delta AMH\Rightarrow\dfrac{AB}{BM}=\dfrac{AM}{MH}\Rightarrow\dfrac{AB}{BE}=\dfrac{AM}{MF}\Rightarrow\Delta ABE\sim\Delta AMF\left(c.g.c\right)\Rightarrow\dfrac{AB}{AE}=\dfrac{AM}{AF}\Rightarrow AB.AF=AM.AE\).
d) Gọi T là trung điểm của HC.
Theo tính chất đường trung bình, ta có TF // MC nên TF \(\perp\) AM.
Mà MF \(\perp\) AT nên F là trực tâm của tam giác AMT.
Suy ra \(AF\perp MT\). Mà MT // BH (tính chất đường TB) nên AF \(\perp\) BH.
cảm ơn nha