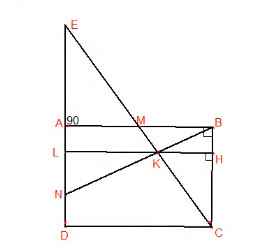
Cho hình chữ nhật ABCD, M là trung điểm của AB, N là trung điểm của AD, MC cắt NB tại E. Biết EMB bằng 10cm2. Tính diện tích ABCD
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


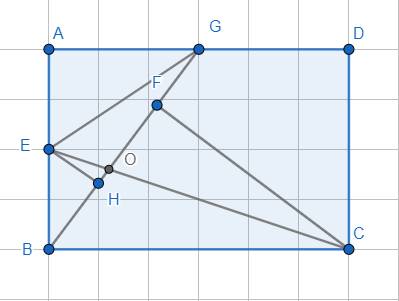
Kẻ \(EH\perp BG\), \(CF\perp BG\)
Ta có: \(S_{ABD}=S_{GBC}=\dfrac{1}{2}.AB.AD=\dfrac{1}{2}.S_{ABCD}\)
\(S_{BAG}=\dfrac{1}{2}.AB.AG=\dfrac{1}{2}.AB.\dfrac{1}{2}AD=\dfrac{1}{4}.AB.AD=\dfrac{1}{2}S_{ABD}\)
\(S_{GEB}=\dfrac{1}{2}.AG.EB=\dfrac{1}{2}.AG.\dfrac{1}{2}.AB=\dfrac{1}{4}.AG.AB=\dfrac{1}{2}S_{ABG}\)
\(\Rightarrow S_{GEB}=\dfrac{1}{2}.\dfrac{1}{2}.\dfrac{1}{2}S_{ABCD}=\dfrac{1}{8}S_{ABCD}=\dfrac{1}{4}S_{GBC}\)
\(\Leftrightarrow\dfrac{1}{2}.EH.BG=\dfrac{1}{4}.\dfrac{1}{2}CF.BG\)
\(\Leftrightarrow EH=\dfrac{1}{4}CF\)
Lại có: \(S_{OBE}=\dfrac{1}{2}OB.EH=\dfrac{1}{2}OB.\dfrac{1}{4}CF=\dfrac{1}{4}S_{OBC}\)
Ta có: \(S_{CBE}=S_{OBE}+S_{OBC}=S_{OBE}+4S_{OBE}=5S_{OBE}\)
\(S_{CBE}=5.10=50\left(cm^2\right)\)
Mà \(S_{CBE}=\dfrac{1}{2}S_{CBA}=\dfrac{1}{4}S_{ABCD}\Rightarrow S_{ABCD}=200\left(cm^2\right)\)

S(ABCD)=600.S(NBC)=S(ABM)=150.S(ABC)=300..S(ANC)=S(AMC)=1/4S(ABCD).
Gọi MH và NI lần lượt là chiều cao của tam giác ANC và AMC.
MH=NI( dt ANC=AMC và chung đáy AC).
S(MFC)=S(NFC)(chung đáy FC và chiều cao MH=NI).
S(MFC)=S(MFB) (chung chiều cao hạ từ Fxuống BC và đáy MC=MB)
suy ra S(FMC)=1/3S(NBC)=1/3× 150
=50.S(AFM)
=S(ABC)-S(FMC)-S(ABM)
=300-50-150=100
S(BMN)=1/4S(ABN)
Gọi MK và AG lần lượt là chiều cao của tam giác BMN và ABN.
Suy ra: MK=1/4AG(▲ BMN=1/4▲ABN và chung đáy NB).
S(MEF)=1/4S(AEF)(chung đáy EF và chiều cao MK=1/4AG) hay S(AEF)=4/5×S(AMF)=4/5×100=80

S(ABCD)=600.S(NBC)=S(ABM)=150.S(ABC)=300..S(ANC)=S(AMC)=1/4S(ABCD). Gọi MH và NI lần lượt là chiều cao của tam giác ANC và AMC. MH=NI( dt ANC=AMC và chung đáy AC). S(MFC)=S(NFC)(chung đáy FC và chiều cao MH=NI). S(MFC)=S(MFB) (chung chiều cao hạ từ Fxuống BC và đáy MC=MB) suy ra S(FMC)=1/3S(NBC)=1/3× 150 =50.S(AFM) =S(ABC)-S(FMC)-S(ABM) =300-50-150=100 S(BMN)=1/4S(ABN) Gọi MK và AG lần lượt là chiều cao của tam giác BMN và ABN. Suy ra: MK=1/4AG( tam giác BMN=1/4tam giác ABN và chung đáy NB). S(MEF)=1/4S(AEF)(chung đáy EF và chiều cao MK=1/4AG) hay S(AEF)=4/5×S(AMF)=4/5×100=80

Ta có: * \(\frac{S_{\Delta ADE}}{S_{\Delta ADB}}=\frac{1}{2}\) mà \(\frac{S_{\Delta ADB}}{S_{ABCD}}=\frac{1}{2}\) suy ra \(\frac{S_{\Delta ADE}}{S_{ABCD}}=\frac{1}{4}\)
* \(\frac{S_{\Delta DCM}}{S_{\Delta DCB}}=\frac{1}{2}\) mà \(\frac{S_{\Delta CDB}}{S_{ABCD}}=\frac{1}{2}\) suy ra \(\frac{S_{\Delta DCM}}{S_{ABCD}}=\frac{1}{4}\)
* \(\frac{S_{\Delta EBM}}{S_{\Delta EBC}}=\frac{1}{2}\) mà \(\frac{S_{\Delta EBC}}{S_{\Delta ABC}}=\frac{1}{2}\) suy ra \(\frac{S_{\Delta EBM}}{S_{\Delta ABC}}=\frac{1}{4}\)
tuy nhiên \(\frac{S_{\Delta EBC}}{S_{ABCD}}=\frac{1}{4}\) suy ra \(\frac{S_{\Delta EBM}}{S_{ABCM}}=\frac{1}{8}\)
Ta lại có: \(\frac{S_{\Delta DEM}}{S_{ABCD}}=S_{ABCD}-\left(S_{\Delta ADE}+S_{\Delta EBM}+S_{\Delta DCM}\right)=1-\left(\frac{1}{4}+\frac{1}{4}+\frac{1}{8}\right)=\frac{3}{8}\)
\(\Rightarrow\) \(S_{ABCD}=S_{\Delta DEM}\div\frac{3}{8}=6\times\frac{8}{3}=16\left(cm^2\right)\)