Giúp em với ạ❤❤❤❤. Em đang cần gấp lắm ạ. Huhu
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



b: \(\sqrt{8^2+6^2}-\sqrt{16}+\dfrac{1}{2}\sqrt{\dfrac{4}{25}}\)
\(=10-4+\dfrac{1}{2}\cdot\dfrac{2}{5}=6+\dfrac{1}{5}=\dfrac{31}{5}\)

\(\left(x:2,2\right)\times\dfrac{1}{6}=\dfrac{-3}{8}\times\left(0,5-1\dfrac{3}{5}\right)\)
\(\Rightarrow\left(x:2,2\right)\times\dfrac{1}{6}=\dfrac{-3}{8}\times\left(\dfrac{1}{2}-\dfrac{8}{5}\right)\)
\(\Rightarrow\left(x:2,2\right)\times\dfrac{1}{6}=\dfrac{-3}{8}\times\dfrac{11}{10}\)
\(\Rightarrow\left(x:2,2\right)\times\dfrac{1}{6}=\dfrac{33}{80}\)
\(\Rightarrow x:2,2=\dfrac{33}{80}:\dfrac{1}{6}\)
\(\Rightarrow x:2,2=\dfrac{99}{40}\)
\(\Rightarrow x=\dfrac{99}{40}\times2,2\)
\(\Rightarrow x=\dfrac{1089}{200}\)
=>(x:2,2)*1/6=-3/8(1/2-8/5)=33/80
=>x:2,2=99/40
=>x=1089/200

1) Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(AH\cdot BC=AB\cdot AC\)
\(\Leftrightarrow AH\cdot10=6\cdot8=48\)
hay AH=4,8(cm)

1:
a: Khi m=1 thì (1) sẽ là x^2+2x-5=0
=>\(x=-1\pm\sqrt{6}\)
b: Δ=(2m)^2-4(-2m-3)
=4m^2+8m+12
=4m^2+8m+4+8=(2m+2)^2+8>=8>0
=>Phương trình luôn có hai nghiệm phân biệt
2:
Thay x=-1 và y=2 vào (P), ta được:
a*(-1)^2=2
=>a=2

Gọi xy là tiếp tuyến tại A của (O)
=>góc xAC=góc ABC
xy//DE
=>góc xAE=góc AED
=>góc AED=góc ABC
Xét ΔAED và ΔABC có
góc AED=góc ABC
góc EAD chung
=>ΔAED đồng dạng với ΔABC
=>AE/AB=AD/AC
=>AE*AC=AB*AD

1 Has - tried
2 Did you go
3 have - been
4 have traveled
5 have been
6 have - finished
7came - told
8 have visted - went - was - haven't visited
9 did you come
10 came
11 Did you watch
12 have - left
13 have - known
14 met - have known
15 happened
16 Did you read
cái này mình có đáp án là:
1.Has-tried
2.did you go
3.have-been
4.have travelend
5.have been
mình làm 5 câu thui nha. Chúc bạn học tốt

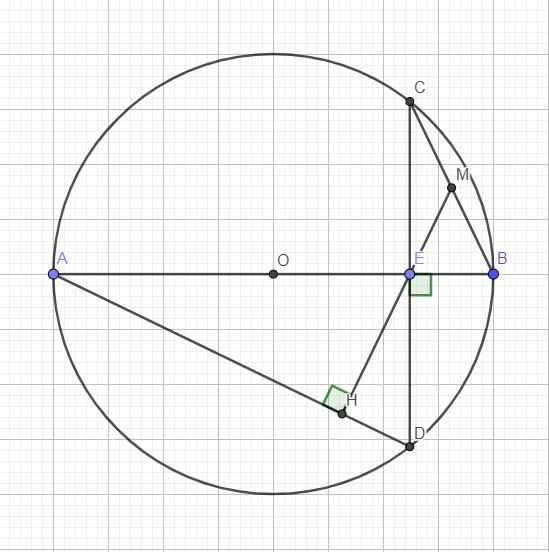
Tứ giác ACBD nội tiếp \(\Rightarrow\widehat{ADC}=\widehat{ABC}\) (cùng chắn AC) (1)
Lại có \(\widehat{ADC}+\widehat{DEH}=90^0\) (tam giác DEH vuông tại H theo gt) (2)
Gọi M là trung điểm BC, nối EM
Trong tam giác vuông BCE, EM là trung tuyến ứng với cạnh huyền
\(\Rightarrow EM=\dfrac{1}{2}BC=BM\Rightarrow\Delta BEM\) cân tại M
\(\Rightarrow\widehat{ABC}=\widehat{MEB}\) (3)
\(\left(1\right);\left(2\right);\left(3\right)\Rightarrow\widehat{DEH}+\widehat{MEB}=90^0\)
\(\Rightarrow\widehat{DEH}+\widehat{MEB}+\widehat{DEB}=90^0+90^0=180^0\)
\(\Rightarrow M;E;H\) thẳng hàng hay HE đi qua trung điểm M của BC

26.
\(\sqrt{\dfrac{-3}{2a^3}}=\sqrt{\dfrac{-3a}{2a^4}}=\dfrac{1}{a^2}\sqrt{\dfrac{-3a}{2}}\)
Đáp án B
28.
\(\sqrt{\dfrac{a^3}{a}}=\sqrt{a^2}=\left|a\right|=-a\)
Đáp án B

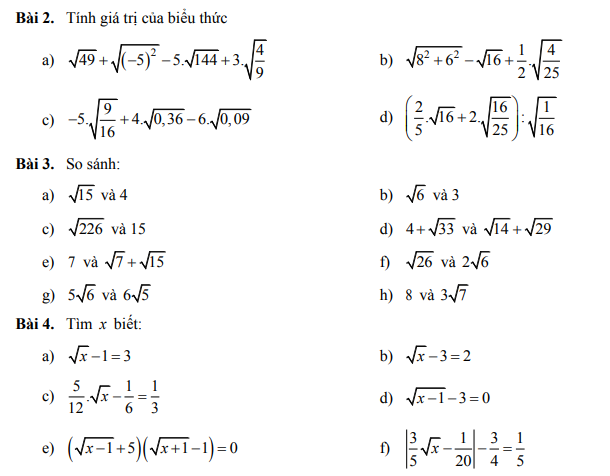 các bạn giúp mình với mình đang cần gấp nên làm bài nào hay bài đấy
các bạn giúp mình với mình đang cần gấp nên làm bài nào hay bài đấy