Cho tam giác ABC vuông tại A, đường cao AH. Trên cạnh AB, AC lấy các điểm M, N sao cho AM = AN = AH; đường phân giác trong góc BAH và CAH cắt MN tại I, J. HI cắt AB tại E, MN cắt AH tại F. Chứng minh EF song song với CJ.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
7 tháng 4 2022
a: Xét ΔABC vuông tại A và ΔHBA vuông tại H có
góc B chung
Do đó: ΔABC\(\sim\)ΔHBA
Xét ΔABC vuông tại A có AH là đường cao
nên \(\dfrac{1}{AH^2}=\dfrac{1}{AB^2}+\dfrac{1}{AC^2}\)
hay AH=16,8(cm)
b: Xét ΔABC vuông tại A có AH là đường cao
nên \(AH^2=HB\cdot HC\)
3 tháng 1 2021
a) Xét ΔCAM có CA=CM(gt)
nên ΔCAM cân tại C(Định nghĩa tam giác cân)
hay \(\widehat{CAM}=\widehat{CMA}\)(hai góc ở đáy)(3)
b) Vì tia AM nằm giữa hai tia AB,AC
nên ta có: \(\widehat{BAM}+\widehat{CAM}=\widehat{BAC}\)
\(\Leftrightarrow\widehat{CAM}+\widehat{NAM}=90^0\)
hay \(\widehat{CAM}\) và \(\widehat{MAN}\) là hai góc phụ nhau(đpcm)
c) Ta có: tia AM nằm giữa hai tia AB,AC
nên \(\widehat{CAM}+\widehat{BAM}=\widehat{BAC}\)
hay \(\widehat{CAM}+\widehat{BAM}=90^0\)(1)
Xét ΔAHM vuông tại H có
\(\widehat{HAM}+\widehat{HMA}=90^0\)(hai góc nhọn phụ nhau)
hay \(\widehat{HAM}+\widehat{CMA}=90^0\)(2)
Từ (1), (2) và (3) suy ra \(\widehat{HAM}=\widehat{BAM}\)
mà tia AM nằm giữa hai tia AB,AH
nên AM là tia phân giác của \(\widehat{BAH}\)(đpcm)
d) Xét ΔAHM và ΔANM có
AH=AN(gt)
\(\widehat{HAM}=\widehat{NAM}\)(cmt)
AM chung
Do đó: ΔAHM=ΔANM(c-g-c)
nên \(\widehat{AHM}=\widehat{ANM}\)(hai góc tương ứng)
mà \(\widehat{AHM}=90^0\)(AH\(\perp\)HM)
nên \(\widehat{ANM}=90^0\)
hay MN\(\perp\)AB(đpcm)
12 tháng 5 2023
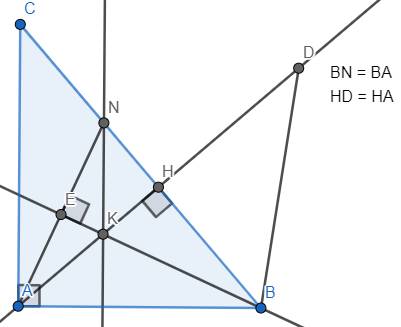
a) Xét ΔABE vuông tại E & ΔNBE vuông tại E có:
- BE là cạnh chung, BN = BA (giả thuyết)
Suy ra ΔABE = ΔNBE (cạnh huyền - cạnh góc vuông)
b) Theo đề ta có BH vuông góc với AD và HA = HD
Suy ra BH là đường trung trực của AD
Suy ra BA = BD (vì B nằm trên đường trung trực của AD)
c) Trong ΔNAB có AH và BE là đường cao, đồng quy tại điểm K
Suy ra NK là đường cao của ΔNAB, hay NK vuông góc với AB
Mà AC cũng vuông góc với AB, suy ra NK // CA
13 tháng 5 2023
a. - Vì BE vuông góc với AN (gt)
=> tam giác ABE vuông tại E (tc)
tam giác NBE vuông tại E (tc)
- Xét tam giác vuông ABE và tam giác vuông NBE, có:
+ Chung BE
+ BA = BN (gt)
=> tam giác vuông ABE = tam giác vuông NBE (Cạnh huyền - cạnh góc vuông)
b. - Vì AH là đường cao của tam giác ABC (gt)
=> tam giác ABH vuông tại H
tam giác DBH vuông tại H
- Xét tam giác vuông ABH và tam giác vuông DBH, có:
+ Chung BH
+ HA = HD (gt)
=> tam giác vuông ABH = tam giác vuông DBH (2 cạnh góc vuông)
=> BA = BD (2 cạnh tương ứng)
6 tháng 7 2023
a: góc BAE+góc CAE=90 độ
góc BEA+góc HAE=90 độ
mà góc CAE=góc HAE
nên góc BAE=góc BEA
=>ΔBAE cân tại B
c: góc CAD+góc BAD=90 độ
góc CDA+góc HAD=90 độ
mà góc BAD=góc HAD
nên góc CAD=góc CDA
=>ΔCAD cân tại C