Giúp Em phần 3,4,5 với ạ em cảm ơn
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


ĐKXĐ:
3.
\(cos\left(3x-\dfrac{\pi}{4}\right)\ne0\Leftrightarrow3x-\dfrac{\pi}{4}\ne\dfrac{\pi}{2}+k\pi\)
\(\Leftrightarrow3x\ne\dfrac{3\pi}{4}+k\pi\Rightarrow x\ne\dfrac{\pi}{4}+\dfrac{k\pi}{3}\)
4.
\(sin\left(2x+\dfrac{\pi}{6}\right)\ne0\Leftrightarrow2x+\dfrac{\pi}{6}\ne k\pi\)
\(\Rightarrow x\ne-\dfrac{\pi}{12}+\dfrac{k\pi}{2}\)
5.
\(\left\{{}\begin{matrix}cosx\ne0\\sin3x\ne0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x\ne\dfrac{\pi}{2}+k\pi\\3x\ne k\pi\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}x\ne\dfrac{\pi}{2}+k\pi\\x\ne\dfrac{k\pi}{3}\end{matrix}\right.\)


a: Xét ΔODB vuông tại D vàΔOCA vuông tại C có
OB=OA
góc O chung
=>ΔODB=ΔOCA
b: ΔODB=ΔOCA
=>góc OBD=góc OAC
góc OBD+góc IBA=góc OBA
góc OAC+góc IAB=góc OAB
mà góc OBD=góc OAC và góc OAB=góc OBA
nên góc IAB=góc IBA
=>ΔIAB cân tại I
c: IC=ID
ID<IA
=>IC<IA


Đây bn nhé:
Ta có a/3 = b/8= c/5. Áp dụng tính chất dãy tỉ số bằng nhau ta có:
2a+3b-c/2.3+3.8-5 = 2a+3b-c/6+24-5 = 50/25 = 2
=> a/3 = 2 => a=6
=> b/8 = 2 => b=16
=> c/5 = 2 => c=10
Nhìn ngắn vậy thôi chứ ko sai đâu bn
Chúc bn học tốt^^
\(\dfrac{a}{3}\) = \(\dfrac{b}{8}\) = \(\dfrac{c}{5}\) và 2a + 3b - c = 50
=> \(\dfrac{2a}{6}\) = \(\dfrac{3b}{24}\) = \(\dfrac{c}{5}\) và 2a + 3b - c = 50
Áp dụng tính chất dãy tỉ số bằng nhau ta có:
\(\dfrac{2a}{6}\) = \(\dfrac{3b}{24}\) = \(\dfrac{c}{5}\) = \(\dfrac{2a+3b-c}{6+24-5}\) = \(\dfrac{50}{25}\) = 2
Vậy:
\(\dfrac{2a}{6}=2\) => \(2a=2.6=12\) => \(a=12:2=6\)
\(\dfrac{3b}{24}=2\) => \(3b=2.24=48\) => \(b=48:3=16\)
\(\dfrac{c}{5}=2\) => \(c=2.5=10\)

\(a^3b-ab^3=ab\left(a^2-b^2\right)=ab\left(a^2-ab+ab-b^2\right)=ab\left(a-b\right)\left(a+b\right)\)
Với a hoặc b chẵn \(\Leftrightarrow ab\left(a-b\right)\left(a+b\right)⋮2\)
Với a và b lẻ \(\Leftrightarrow\left(a-b\right)⋮2\Leftrightarrow ab\left(a-b\right)\left(a+b\right)⋮2\)
Vậy \(ab\left(a-b\right)\left(a+b\right)⋮2,\forall a,b\left(1\right)\)
Với a hoặc b chia hết cho 3 thì \(ab\left(a-b\right)\left(a+b\right)⋮3\)
Với \(a=3k+1;b=3q+1\Leftrightarrow\left(a-b\right)=3\left(k-q\right)⋮3\)
\(\Leftrightarrow ab\left(a-b\right)\left(a+b\right)⋮3\)
Với \(a=3k+1;b=3q+2\Leftrightarrow\left(a+b\right)=\left(3k+1+3q+2\right)=3\left(k+q+1\right)⋮3\)
\(\Leftrightarrow ab\left(a-b\right)\left(a+b\right)⋮3\)
Mà a,b có vai trò tương đương nên \(ab\left(a-b\right)\left(a+b\right)⋮3,\forall a,b\left(2\right)\)
\(\left(1\right)\left(2\right)\Leftrightarrowđpcm\)
Ta có : a3b -ab3
=a3b -ab -ab3 +ab
=ab (a2 -1) -ab (b2 -1)
=ab (a-1)(a+1) -ab (b-1)(b+1)
Vì a (a-1)(a+1) là 3 số tự nhiên liên tiếp nên chia hết cho 6 .Tương tự b (b-1)(b+1) cũng chia hết cho 6
=> a3b -ab3 chia hết cho 6 (đpcm )






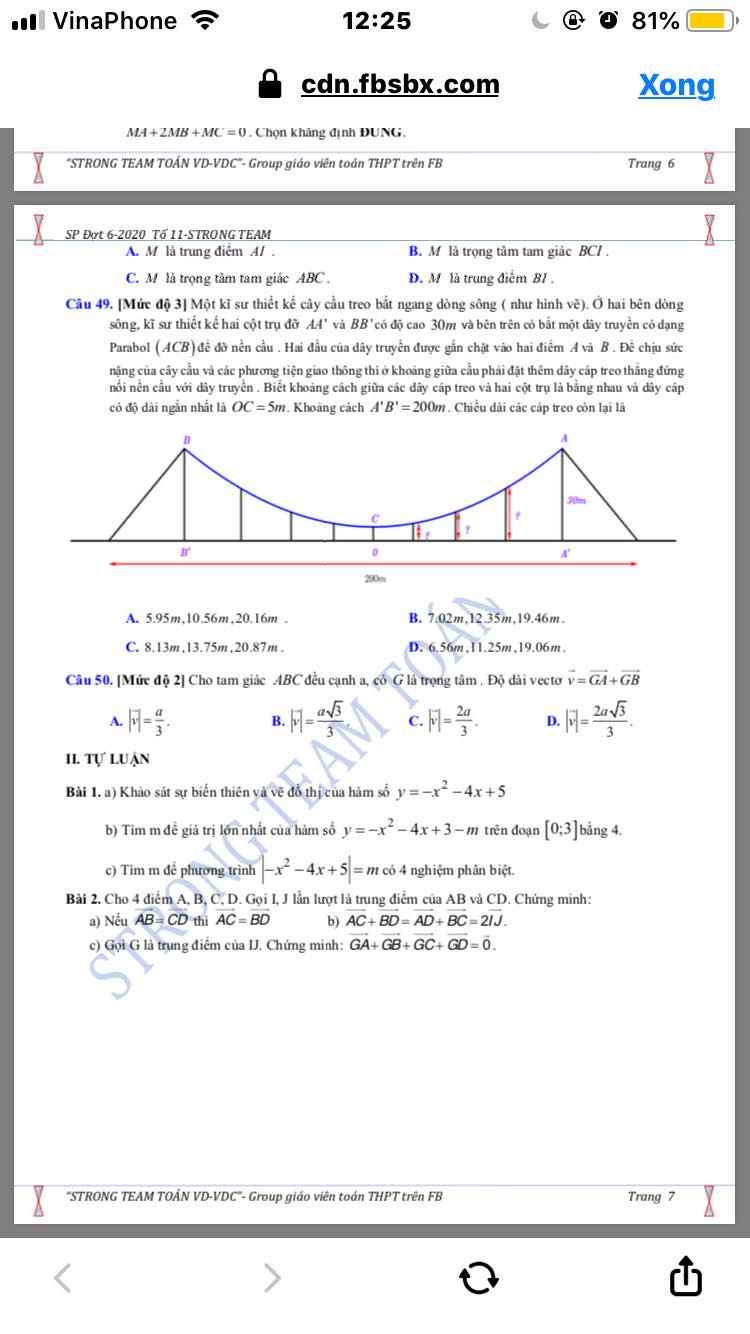 nhiều
nhiều


3/ Bạn chứng minh \(AK\perp BE\)tại K bằng cách tương tự câu a (bạn này đã làm được câu này rồi phải không?)
\(\Rightarrow\)AK là đường cao của \(\Delta ABE\)
Theo câu a, ta sẽ có \(BC\perp AE\)tại C \(\Rightarrow\)BC là đường cao của \(\Delta ABE\)
Xét \(\Delta ABE\)có hai đường cao AK và BC cắt nhau tại H \(\Rightarrow\)H là trực tâm \(\Delta ABE\)\(\Rightarrow EH\perp AB\left(đpcm\right)\)
5/ Vì E đối xứng với A qua C nên C là trung điểm AE, từ đó BC là trung tuyến của \(\Delta ABE\)
Xét \(\Delta ABE\)có BC vừa là đường cao vừa là trung tuyến \(\Rightarrow\Delta ABE\)cân tại B