
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Bài 3:
a: Gọi OK là khoảng cách từ O đến AB
Suy ra: K là trung điểm của AB
hay \(AK=BK=\dfrac{AB}{2}=\dfrac{8}{2}=4\left(cm\right)\)
Áp dụng định lí Pytago vào ΔOKA vuông tại K, ta được:
\(OA^2=OK^2+KA^2\)
hay OK=3(cm)

1) \(x^4-10x^2+1=0\)
\(\Leftrightarrow\left(x^2-5\right)^2=24\)
\(\Leftrightarrow\left[{}\begin{matrix}x^2-5=2\sqrt{6}\\x^2-5=-2\sqrt{6}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\sqrt{5+2\sqrt{6}}\\x=\sqrt{5-2\sqrt{6}}\end{matrix}\right.\)\(\Leftrightarrow\left[{}\begin{matrix}x=\sqrt{\left(\sqrt{3}+\sqrt{2}\right)^2}\\x=\sqrt{\left(\sqrt{3}-\sqrt{2}\right)^2}\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=\sqrt{3}+\sqrt{2}\\x=\sqrt{3}-\sqrt{2}\end{matrix}\right.\)
Vậy \(x=\sqrt{2}+\sqrt{3}\) là một nghiệm của pt
2) Ta có: \(a-b=\sqrt{3}+1,b-c=\sqrt{3}-1\)
\(\Rightarrow a-c=a-b+b-c=\sqrt{3}+1+\sqrt{3}-1=2\sqrt{3}\)
\(A=a^2+b^2+c^2-ab-bc-ac\)
\(\Rightarrow2A=2a^2+2b^2+2c^2-2ab-2ac-2bc\)
\(=\left(a^2-2ab+b^2\right)+\left(b^2-2bc+c^2\right)+\left(a^2-2ac+c^2\right)\)
\(=\left(a-b\right)^2+\left(b-c\right)^2+\left(a-c\right)^2\)
\(\left(\sqrt{3}+1\right)^2+\left(\sqrt{3}-1\right)^2+\left(2\sqrt{3}\right)^2\)
\(=3+2\sqrt{3}+1+3-2\sqrt{3}+1+12=20\)
\(\Rightarrow A=10\in N\)


Bài 4:
2: Xét ΔBAK vuông tại A có AD là đường cao ứng với cạnh huyền BK
nên \(BD\cdot BK=BA^2\left(1\right)\)
Xét ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC
nên \(BH\cdot BC=BA^2\left(2\right)\)
Từ (1) và (2) suy ra \(BD\cdot BK=BH\cdot BC\)

Bài 5:
\(\cos\alpha=\sqrt{1-\dfrac{1}{25}}=\dfrac{2\sqrt{6}}{5}\)
\(\tan\alpha=\dfrac{1}{5}:\dfrac{2\sqrt{6}}{5}=\dfrac{1}{2\sqrt{6}}=\dfrac{\sqrt{6}}{24}\)
\(\cot\alpha=1:\dfrac{\sqrt{6}}{24}=4\sqrt{6}\)

a) Ta có: \(B=\dfrac{2x+3\sqrt{x}+9}{x-9}-\dfrac{\sqrt{x}}{\sqrt{x}+3}\)
\(=\dfrac{2x+3\sqrt{x}+9-x+3\sqrt{x}}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(=\dfrac{x+6\sqrt{x}+9}{\left(\sqrt{x}-3\right)\left(\sqrt{x}+3\right)}\)
\(=\dfrac{\sqrt{x}+3}{\sqrt{x}-3}\)



 , mình đang cần giải gấp. Cảm ơn mn nhiều.
, mình đang cần giải gấp. Cảm ơn mn nhiều.




 Giúp em với ạ, em cảm ơn ạ
Giúp em với ạ, em cảm ơn ạ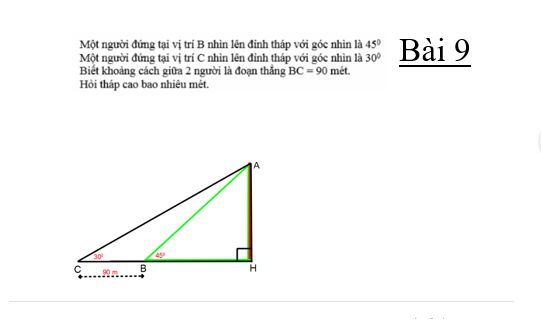 giúp em với ạ. Em cảm ơn ạ
giúp em với ạ. Em cảm ơn ạ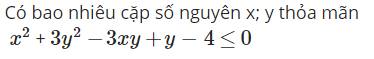

3/ Bạn chứng minh \(AK\perp BE\)tại K bằng cách tương tự câu a (bạn này đã làm được câu này rồi phải không?)
\(\Rightarrow\)AK là đường cao của \(\Delta ABE\)
Theo câu a, ta sẽ có \(BC\perp AE\)tại C \(\Rightarrow\)BC là đường cao của \(\Delta ABE\)
Xét \(\Delta ABE\)có hai đường cao AK và BC cắt nhau tại H \(\Rightarrow\)H là trực tâm \(\Delta ABE\)\(\Rightarrow EH\perp AB\left(đpcm\right)\)
5/ Vì E đối xứng với A qua C nên C là trung điểm AE, từ đó BC là trung tuyến của \(\Delta ABE\)
Xét \(\Delta ABE\)có BC vừa là đường cao vừa là trung tuyến \(\Rightarrow\Delta ABE\)cân tại B