Chứng minh rằng: ab + 8. ba chia hết cho 9.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
1 tháng 10 2023
a, 10615 + 8 không chia hết cho 2 vì 8 ⋮ 2 nhưng 10615 không chia hết cho 2
10615 + 8 không chia hết cho 9 vì 1 + 6 + 1 + 5 + 8 = 21 không chia hết cho 9
NT
Nguyễn Thị Thương Hoài
Giáo viên
VIP
1 tháng 10 2023
c, B = 102010 - 4
10 \(\equiv\) 1 (mod 3)
102010 \(\equiv\) 12010 (mod 3)
4 \(\equiv\) 1(mod 3)
⇒ 102010 - 4 \(\equiv\) 12010 - 1 (mod 3)
⇒ 102010 - 4 \(\equiv\) 0 (mod 3)
⇒ 102010 - 4 \(⋮\) 3
16 tháng 2 2022
a)ab+ba
Ta có:ab=10a+b
ba=10b+a
ab+ba=10a+b+10b+a
= 11a + 11b
Ta thấy: 11a⋮11 ; 11b⋮11
=>ab+ba⋮11 (ĐPCM)
b)ab-ba⋮9
Ta có:ab=10a+b
ba=10b+a
ab+ba=10a+b-10b+a
= 9a - 9b
Ta thấy: 9a⋮9 ; 9b⋮9
=>ab+ba⋮9 (ĐPCM)
PT
1
CM
6 tháng 7 2018
a, a b + b a = (10a+b)+(10b+a) = 11a+11b = 11.(a+b) ⋮ 11
b, a b - b a = (10a+b) - (10b+a) = 9a - 9b = 9(a - b) ⋮ 9 (a>b)
NB
2
PN
2 tháng 5 2016
Theo đề ta có: ab + 8.ba = 10a+b + 8.(10b+a)
= 10a+b + 80b+8a
= 18a + 81b
Ta có: 18 chia hết cho 9 => 18a chia hết cho 9
81 chia hết cho 9 => 81b chia hết cho 9
Vì: 18a chia hết cho 8 và 81b chia hết cho 9
=> 18a + 81b chia hết cho 9
Vậy ab + 8.ba chia hết cho 9.
chú thích: bạn viết dấu chia hết cho nhanh
cái đoạn Ta có:..... khỏi cần viết cũng được
NT
1
16 tháng 2 2022
a)ab+ba
Ta có:ab=10a+b
ba=10b+a
ab+ba=10a+b+10b+a
= 11a + 11b
Ta thấy: 11a⋮11 ; 11b⋮11
=>ab+ba⋮11 (ĐPCM)
b)ab-ba⋮9
Ta có:ab=10a+b
ba=10b+a
ab+ba=10a+b-10b+a
= 9a - 9b
Ta thấy: 9a⋮9 ; 9b⋮9
=>ab+ba⋮9 (ĐPCM)
CM
21 tháng 6 2019
Sơ đồ con đường |
Lời giải chi tiết |
Bước 1. Phân tích cấu tạo số Bước 2. Áp dụng tính chất chia hết của một tích. |
Ta có: a b ¯ − b a ¯ = 10 a + b − 10 b − a = 9 a − 9 b = 9 a − b Áp dụng tính chất chia hết của một tích ta có: 9 a − b ⋮ 9 ⇒ a b ¯ − b a ¯ ⋮ 9 Vậy a b ¯ − b a ¯ chia hết cho 9. |
2 tháng 5 2017
ab+83ba=10a+b+8.b.10+8a.
=(10a+8a)+(80b+b).
=18a+81b.
=9.(2a+9b).
Đến đây dễ rồi tự làm tiếp nha
2 tháng 5 2017
Theo bài ta có:
ab + 8.ba
= 10.a + b + 8.(10b + a)
= 10.a + b + 80.b + 8.a
= 18.a + 81.b
Ta có:
+ 18 \(⋮\)9
\(\Rightarrow\)18.a \(⋮\)9
+ 81 \(⋮\)9
\(\Rightarrow\)81.b \(⋮\)9
Vì 18.a \(⋮\)9 và 81.b \(⋮\)9
\(\Rightarrow\)18.a + 81.b chia hết cho 9
\(\Rightarrow\)ab + 8.ba chia hết cho 9.
TQ
3
SN
28 tháng 6 2015
đặt c = a+ b
ta có: ab¯ + ba¯ =cc¯
mà cc¯ chia hết cho 11 ( cc¯:11=c)
ab=10*a+b
ba=10*b+a
ab-ba=9*a-9*b=9*(a-b)=> ab-ba chia hết cho 9
27 tháng 9 2016
ab+ba=10a + b +10b + a = 11a + 11b = 11 (a+b) chia hết cho 111
tớ chỉ giải đc 1 câu thôi còn câu b tịt
26 tháng 8 2017
a) Ta có : ab - ba
=> a . 10 + b - b . 10 + a
=> ( a . 10 ) - a + ( 10 . b ) - b
=> 9. a + 9 . b
=> 9 . ( a + b ) chia hết cho 9 ( đpcm)
đpcm là điều phải chứng minh nha bạn
Câu b ban làm tương nha
Chúc bạn học giỏi
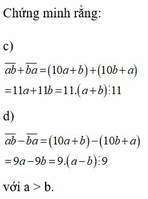
Ta có: ab + 8.ba = 10a + b + 8.(10b + a)
= 10a + b + (8.10b) + (8.a)
= 10a + b + 80b + 8a
= (10a + 8a) + (80b+b)
= 18a + 81b
Vì: * 18 ⋮ 9 => 18a ⋮ 9 ( 1 )
* 81⋮ 9 => 81b ⋮ 9 ( 2 )
Tù ( 1 ) và ( 2 ) => 18a + 81b ⋮ 9
10a+b + 8 . ( 10b+a)
10a +b + 80b+8a
10a+8a+ 80b+b
18a + 81b chia hết cho 9
chắc vậy