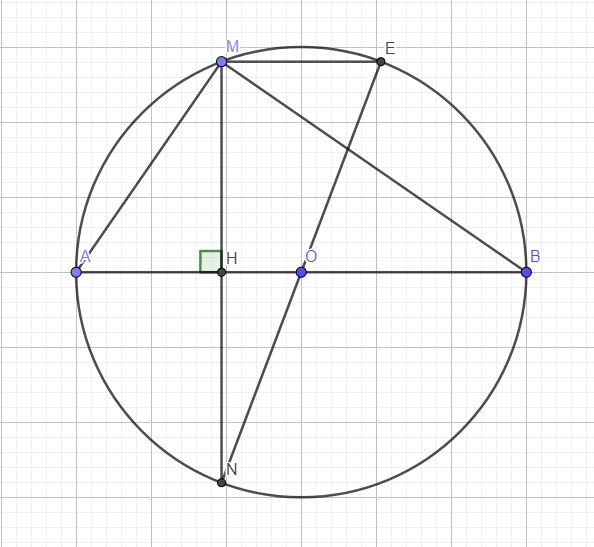
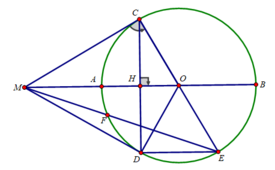
Cho (O) đường kính AB. M e (O)/ MA <MB. Tia p/g góc AMB cắt AB tại C. Qua C kẻ đường vuông góc với AB cắt AM,BM tại D,H.
a) HE vuông góc với tiếp tuyến tại A của (O). C/m ACHE là hv
b) DF vuông góc với tiếp tuyến tại B của (O). c/m E,M,N,F thẳng hàng