Tính giới hạn sau: l i m x → ∞ 2 x - 1 1 - x ?
A. 1
B. 2
C. -1
D. -2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
NV
Nguyễn Việt Lâm
Giáo viên
12 tháng 4 2020
Do \(x< 2\) nên x chỉ tiến tới 2 từ phía trái
Do đó hàm số chỉ có giới hạn trái tại điểm x=2 (giới hạn bằng dương vô cực)
CM
11 tháng 8 2017
a) Đáp số: 1/6
b) Đáp số: 937/12.
Hướng dẫn:
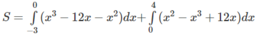
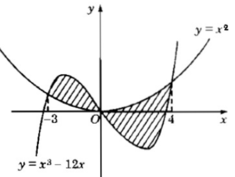
c) Đáp số: 2
Hướng dẫn: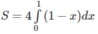 
d) π/2 - 1
Hướng dẫn:
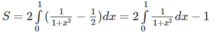
Đặt x = tan t để tính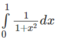 
e) Đáp số: 27/4
Hướng dẫn: Phương trình tiếp tuyến tại (-1; -2) là y = 3x + 1. Do đó, diện tích :
NV
Nguyễn Việt Lâm
Giáo viên
25 tháng 2 2020
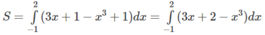
Đáp án D sai
Hàm đa thức có giới hạn tại mọi điểm và tại tất cả các điểm thì giới hạn trái luôn bằng giới hạn phải
AH
Akai Haruma
Giáo viên
8 tháng 3 2021
Đề bị lỗi công thức rồi bạn. Bạn cần viết lại để được hỗ trợ tốt hơn.
NV
Nguyễn Việt Lâm
Giáo viên
25 tháng 2 2020
Đáp án A đúng
Đáp án B hàm số có giới hạn phải tại 2 nhưng ko có giới hạn trái tại 2
Đáp án C có giới hạn trái tại 2 nhưng ko có giới hạn phải tại 2
Đáp án D giới hạn trái tại 2 bằng âm vô cùng, giới hạn phải tại 2 bằng dương vô cùng
TG
28 tháng 11 2019
Câu 1: đoạn thẳng có đặc điểm nào trong các điểm sau
A giới hạn ở 1 đầu.
B kéo dài mãi về 1 phía
C giới hạn ở 2 đầu
D kéo dài mãi về 2 phía
Câu 2: Trong các cách viết sau cách nào sử dụng sai kí hiệu
A .m ∉ A
B .a ∈ b
C .N ∉ xy
D.m ∈ a
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 5 2020
d.
\(\lim\limits_{x\rightarrow\infty}\frac{2x+1}{x+1}=2\Rightarrow y=2\) là TCN của (C)
Diện tích:
\(S=\int\limits^3_1\left(2-\frac{2x+1}{x+1}\right)dx=\int\limits^3_1\frac{1}{x+1}dx=ln\left|x+1\right||^3_1=ln4-ln2=ln2\)
e.
Pt hoành độ giao điểm:
\(2-x^2=x\Leftrightarrow x^2+x-2=0\Rightarrow\left[{}\begin{matrix}x=1\\x=-2\end{matrix}\right.\)
Diện tích:
\(S=\int\limits^1_{-2}\left(2-x^2-x\right)dx=\left(2x-\frac{1}{3}x^3-\frac{1}{2}x^2\right)|^1_{-2}=\frac{9}{2}\)
NV
Nguyễn Việt Lâm
Giáo viên
10 tháng 5 2020
a. Pt hoành độ giao điểm: \(\frac{e^x\left(1+x\right)}{1+xe^x}=0\Rightarrow x=-1\)
Diện tích:
\(S=\int\limits^0_{-1}\frac{e^x+xe^x}{1+xe^x}dx\)
Đặt \(1+xe^x=t\Rightarrow\left(e^x+xe^x\right)dx=dt\) ; \(\left\{{}\begin{matrix}x=-1\Rightarrow t=1-\frac{1}{e}\\x=0\Rightarrow t=1\end{matrix}\right.\)
\(S=\int\limits^1_{1-\frac{1}{e}}\frac{dt}{t}=ln\left|t\right||^1_{1-\frac{1}{e}}=-ln\left|\frac{e-1}{e}\right|=ln\left(\frac{e}{e-1}\right)\)
b. Đồ thị \(y=3^x\) ko cắt trục hoành
Diện tích:
\(S=\int\limits^2_03^xdx=\frac{3^x}{ln3}|^2_0=\frac{9}{ln3}-\frac{1}{ln3}=\frac{8}{ln3}\)
c.
Pt hoành độ giao điểm:
\(x^4-4x^2+4=x^2\Leftrightarrow x^4-5x^2+4=0\Rightarrow\left[{}\begin{matrix}x^2=1\\x^2=4\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=1\\x=2\end{matrix}\right.\)
Diện tích:
\(S=\int\limits^1_0\left(x^4-4x^2+4-x^2\right)dx=\int\limits^1_0\left(x^4-5x^2+4\right)dx\)
\(=\left(\frac{1}{5}x^5-\frac{5}{3}x^3+4x\right)|^1_0=\frac{38}{15}\)
NV
Nguyễn Việt Lâm
Giáo viên
17 tháng 5 2020
Đáp án A, khi \(x\rightarrow1\) thì \(x-2< 0\) nên biểu thức không xác định
\(\Rightarrow\) Giới hạn đã cho ko tồn tại
Chọn D.