Hàm số y = - x 3 + 3 x 2 - 1 đồng biến trên khoảng:
A. 0 ; 2
B. - ∞ ; 1
C. ℝ
D. - ∞ ; 0 , 2 ; + ∞
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

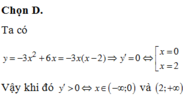

1.
\(y'=2cosx-2sin2x=2cosx-4sinx.cosx=2cosx\left(1-2sinx\right)\)
\(y'=0\Rightarrow\left[{}\begin{matrix}cosx=0\\sinx=\dfrac{1}{2}\end{matrix}\right.\) \(\Rightarrow\left[{}\begin{matrix}x=\dfrac{\pi}{2}\\x=\dfrac{\pi}{6}\\x=\dfrac{5\pi}{6}\end{matrix}\right.\)
Hàm đồng biến trên các khoảng \(\left(0;\dfrac{\pi}{6}\right)\) và \(\left(\dfrac{\pi}{2};\dfrac{5\pi}{6}\right)\)
2.
Xét hàm \(f\left(x\right)=x^2-2x-3\)
\(f\left(x\right)=0\Rightarrow\left[{}\begin{matrix}x=-1\\x=3\end{matrix}\right.\)
\(f'\left(x\right)=2x-2=0\Rightarrow x=1\)
Hàm nghịch biến trên các khoảng \(\left(-\infty;-1\right)\) và \(\left(1;3\right)\)

1: TXĐ: D=R\{3}
\(y=\dfrac{x^2-6x+10}{x-3}\)
=>\(y'=\dfrac{\left(x^2-6x+10\right)'\left(x-3\right)-\left(x^2-6x+10\right)\left(x-3\right)'}{\left(x-3\right)^2}\)
=>\(y'=\dfrac{\left(2x-6\right)\left(x-3\right)-\left(x^2-6x+10\right)}{\left(x-3\right)^2}\)
=>\(y'=\dfrac{2x^2-12x+18-x^2+6x-10}{\left(x-3\right)^2}\)
=>\(y'=\dfrac{x^2-6x+8}{\left(x-3\right)^2}\)
Đặt y'<=0
=>\(\dfrac{x^2-6x+8}{\left(x-3\right)^2}< =0\)
=>\(x^2-6x+8< =0\)
=>(x-2)(x-4)<=0
=>2<=x<=4
Vậy: Khoảng đồng biến là [2;3) và (3;4]

1.
\(f'\left(x\right)=\left(x^2-1\right)\left(x-2\right)^2\left(x-3\right)\) có các nghiệm bội lẻ \(x=\left\{-1;1;3\right\}\)
Sử dụng đan dấu ta được hàm đồng biến trên các khoảng: \(\left(-1;1\right);\left(3;+\infty\right)\)
Hàm nghịch biến trên các khoảng \(\left(-\infty;-1\right);\left(1;3\right)\)
2.
\(y'=4x^3-4x=0\Rightarrow\left[{}\begin{matrix}x=-1\\x=0\\x=1\end{matrix}\right.\)
Lập bảng xét dấu y' ta được hàm đồng biến trên \(\left(-1;0\right);\left(1;+\infty\right)\)
Hàm nghịch biến trên \(\left(-\infty;-1\right);\left(0;1\right)\)

Đáp án là C
I.Sai ví dụ hàm số y = x 3 đồng biến trên
(−¥; +¥) nhưng y' ³ 0, "x Î (−¥; +¥)
II.Đúng
III.Đúng

Đáp án D
Phương pháp: +) Khảo sát sự biến thiên của đồ thị hàm số.
+) Hàm số đạt cực trị tại điểm x = x 0 ⇔ y ' x 0 = 0 và x = x 0 được gọi là điểm cực trị.
+) Hàm số đạt cực trị tại điểm x = x 0 thì y x 0 là giá trị cực trị.

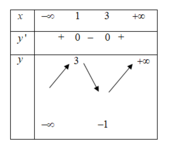

Như vậy có 3 mệnh đề đúng.
Chú ý: Học sinh thường giá trị cực trị và
điểm cực trị nên có thể chọn sai mệnh dề (2) đúng.