Tính diện tích toàn phần (tổng diện tích các mặt) của khối hai mươi mặt đều cạnh a.
K
Khách
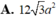
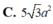
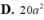
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
21 tháng 6 2017
Đúng(0)
Những câu hỏi liên quan
H9
HT.Phong (9A5)
CTVHS
31 tháng 7 2023
Nữa chu vi đáy của hình chóp đều:
\(8\cdot4:2=16\left(cm\right)\)
Diện tích xung quanh của hình chóp đều:
\(S_{xq}=16\cdot5=80\left(cm^2\right)\)
Diện tích đáy của hình chóp đều:
\(S_đ=8^2=64\left(cm^2\right)\)
Diện tích toàn phần của hình chóp đều:
\(S_{tp}=S_đ+S_{xq}=64+80=144\left(cm^2\right)\)
CM
22 tháng 3 2018
Đáp án C
Diện tích của tam giác đều có cạnh là a bằng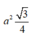 
Ta có: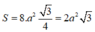 
CM
13 tháng 3 2017
Đáp án C
Diện tích của tam giác đều có cạnh là a bằng a 2 3 4 Ta có S = 8. a 2 3 4 = 2 a 2 3
CM
26 tháng 10 2019
Đáp án B.
Bát diện đều có 8 mặt đều là tam giác đều có cạnh a.
Diện tích tam giác đều có cạnh a là S = 1 2 a . a . sin 60 ^ = 3 4 a 2 ⇒ Tổng diện tích các mặt của khối bát diện đều là 8. 3 4 a 2 = 2 3 a 2 .
31 tháng 7 2023
Sxq=16*4*17/2=544cm2
Stp=544+16^2=800cm2
V=1/3*16^2*15=1280cm3
H9
HT.Phong (9A5)
CTVHS
31 tháng 7 2023
Nữa chu vi đáy của hình chóp đều:
\(16\cdot4:2=32\left(cm\right)\)
Diện tích xung quanh của hình chóp đều:
\(S_{xq}=32\cdot17=544\left(cm^2\right)\)
Diện tích mặt đáy của hình chóp đều:
\(S_đ=16^2=256\left(cm^2\right)\)
Diện tích toàn phần của hình chóp đều:
\(S_{tp}=S_đ+S_{xq}=544+256=800\left(cm^2\right)\)
Thể tích của hình chóp đều:
\(V=\dfrac{1}{3}\cdot256\cdot15=1280\left(cm^3\right)\)