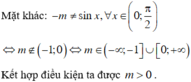Với giá trị nào của m thì hàm số đồng biến trên khoảng
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



+ Tính đạo hàm y ' = cos x + sin x + 2017 2 m .
y ' ≥ 0 ⇔ m ≥ - sin x - cos x 2017 2 = f ( x )
+ Theo bất đẳng thức Bunhiacopxki thì
( - sin x - cos x ) 2 ≤ ( - 1 ) 2 + ( - 1 ) 2 sin 2 x + cos 2 x = 2 - 2 ≤ ( - sin x - cos x ) ≤ 2
Do đó :
- 2 2017 2 ≤ f ( x ) ≤ 2 2017 2
F(x) đạt giá trị lớn nhất là 2 2017 2 = 1 2017 ⇒ m ≥ f ( m a x ) = 1 2017
Chọn C.

Chọn A
Điều kiện: ![]() . Điều kiện cần để hàm số
. Điều kiện cần để hàm số ![]() nghịch biến trên khoảng
nghịch biến trên khoảng ![]() là
là![]() .
.
Ta có : 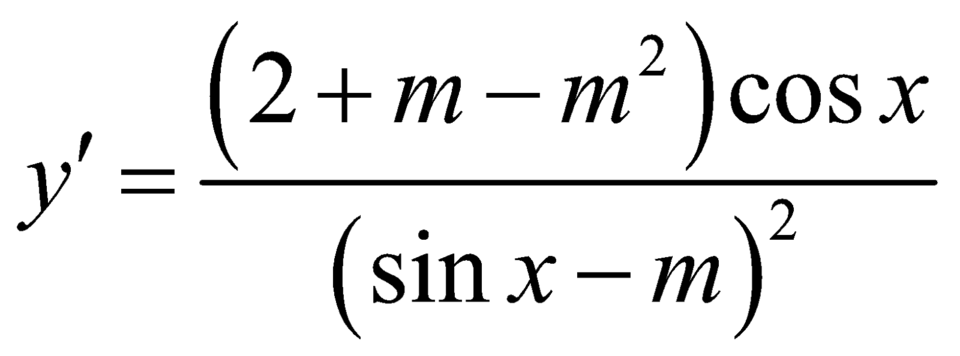 .
.
Ta thấy ![]()
![]() .
.
Để ham số ![]() nghịch biến trên khoảng
nghịch biến trên khoảng ![]() là
là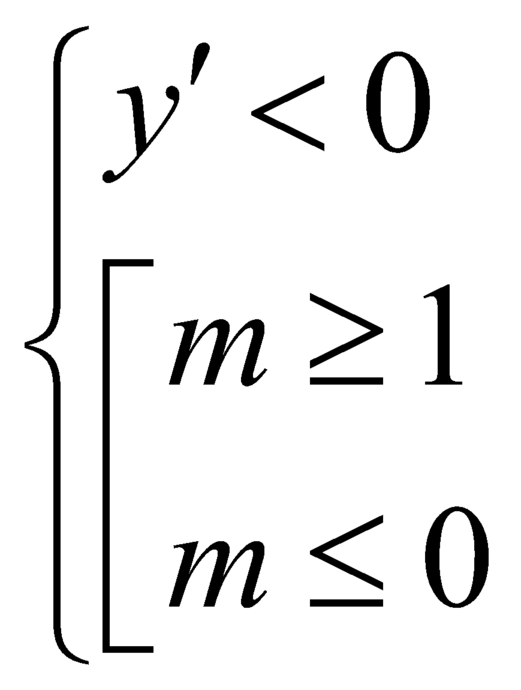
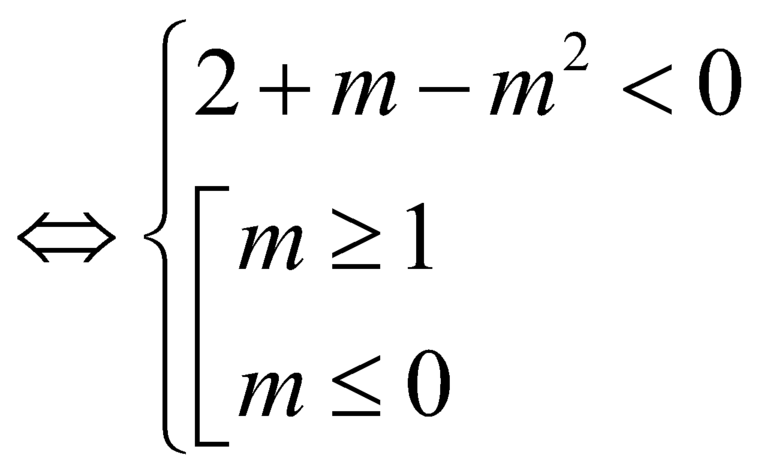
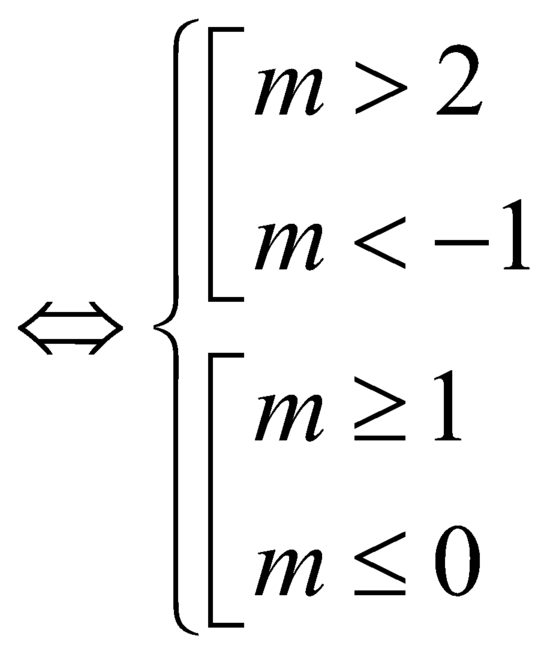
![]() .
.

Đáp án B
Có y ' = − m + 1 cos x sin x − m 2 .
Vì x ∈ 0 ; π 2 ⇒ sin x ∈ 0 ; 1 .
Hàm số xác định trên 0 ; π 2 ⇔ m ∉ 0 ; 1 (1)
Hàm số đồng biến tên 0 ; π 2 ⇔ − m + 1 > 0 ⇔ m < 1 (2)
Kết hợp (1);(2) ta có m ≤ 0 .

y ' = 1 + m cos x - sin x = 1 - 2 m sin x - π 4
Đặt t = sin x - π 4 với t ∈ - 1 ; 1 ta có f 1 = 1 - 2 m t
Để hàm số đồng biến trên R thì
f t ≥ 0 ∀ t ∈ - 1 ; 1 ⇔ f - 1 ≥ 0 f 1 ≥ 0 ⇔ 1 + 2 m ≥ 0 1 - 2 m ≥ 0
⇔ m ≥ - 2 2 m ≤ 2 2 ⇔ - 2 2 ≤ m ≤ 2 2
Đáp án A