Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Ta có: y ' = 3 x 2 + 2 m + 1 x + 3
Hàm số đồng biến trên
R ⇔ y ' ≥ 0 ∀ x ∈ ℝ ⇔ a y ' = 3 > 0 Δ ' y ' = m + 1 2 − 9 ≤ 0 ⇔ − 3 ≤ m + 1 ≤ 3
⇔ − 4 ≤ m ≤ 2.

S là tập con của F trong các trường hợp sau:
TH1: S là tập rỗng, tức là pt x2 - 2x + m = 0 vô nghiệm => delta' = 1 - m < 0 => m > 1
TH2: S có 1 nghiệm kép < 0 => delta' = 1 - m = 0 và nghiệm kép -b'/a = 1 < 0. Điều này không xảy ra
TH3: S có 2 nghiệm đều < 0 => Tổng 2 nghiệm cũng < 0. Mà tổng 2 nghiệm = -b/a = 1 là số dương => Điều này cũng ko bao giờ xảy ra.
Vậy m > 1 thì S là rỗng và khi đó S là tập con của F.

+TXĐ: X\(\in\)R
+y'=\(3x^2-6x\Rightarrow y'=0\Leftrightarrow\int_{x=2;y=0}^{x=0;y=4}\)
+y''=6(x-1)=> y' = 0 khi x = 1;y=2
+
| x | -\(\infty\) 0 1 2 +\(\infty\) |
| y' | + 0 - - 0 + |
| y |

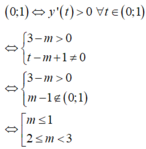



Đáp án B
Có y ' = − m + 1 cos x sin x − m 2 .
Vì x ∈ 0 ; π 2 ⇒ sin x ∈ 0 ; 1 .
Hàm số xác định trên 0 ; π 2 ⇔ m ∉ 0 ; 1 (1)
Hàm số đồng biến tên 0 ; π 2 ⇔ − m + 1 > 0 ⇔ m < 1 (2)
Kết hợp (1);(2) ta có m ≤ 0 .