Cho hình lăng trụ tam giác ABC.A'B'C'. Gọi I, J lần lượt là trọng tâm của các tam giác ABC và A'B'C'. Thiết diện tạo bởi mặt phẳng (AIJ) với hình lăng trụ đã cho là hình gì?
A. Tam giác cân
B. Tam giác vuông
C. Hình thang
D. Hình bình hành
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
CM
8 tháng 4 2019
Đáp án D
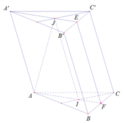
Gọi E và F lần lượt là trung điểm của B’C’ và BC
Xét (AIJ) và (ABC) có: F ∈ AI ⇒ F ∈ (AIJ) ⇒ (AIJ) ∩ (ABC) = AF
Xét ( AIJ) và (B’C’CB) có : F là điểm chung
IJ // (B’C’CB) ( I; J lần lượt là trọng tâm tam giác ABC và A’B’C’)
⇒ giao tuyến của 2 mặt phẳng là đường thẳng a đi qua F và song song IJ
a cắt B’C’ tại E
⇒ (AIJ) ∩ (B’C’CB) = EF
Xét ( AIJ) và (A’B’C’) có:
E là điểm chung
AF // (A’B’C’)
⇒ giao tuyến 2 mặt phẳng là đường thẳng b đi qua E và song song AF
⇒ (AIJ) ∩ (A’B’C’) = A’E
Xét A’EFA có: AA’ // EF ( // IJ)
A’E // AF
A’EFA là hình bình hành
CM
19 tháng 3 2017
Đáp án C
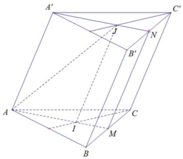
Xét tam giác A’B’C’:
Gọi N là trung điểm B’C’
J là trọng tâm A’B’C’
Xét tam giác ABC:
Gọi M là trung điểm BC
I là trọng tâm ABC
Từ (1), (2), ta có IJ // MN
Xét (AIJ) và (B’C’CB) có:
M là điểm chung
IJ // MN
⇒ giao tuyến của (AIJ) và (B’C’CB) là MN
⇒ thiết diện cần tìm là mặt phẳng (A’NMA)
Xét (A’NMA) có: A’A // MN và A’A = MN ( // = BB’)
A’NMA là hình hình hành
CM
24 tháng 7 2019
Chọn D
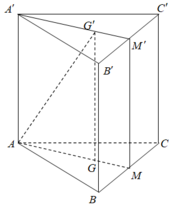
Gọi M, M' lần lượt là trung điểm của BC và B’C’. Khi đó thiết diện của lăng trụ tạo bởi mặt phẳng (AGG') là hình chữ nhật AMM'A’.
Mà A M ’ = a . s i n 60 0 = a 3 2 ≠ A A ’
Nên AMM’A’ không thể là hình vuông.
CM
12 tháng 3 2017
Gọi M là trung điểm BC: BC = 2a; AG = 2 3 AI = 2 a 3 ; A ' A G ^ = 60 o .
Suy ra: A ' G = A G tan 60 o = 2 a 3 3
Ta có: V = S A B C . A ' G = 1 2 AB.AC.A'G
= 1 2 a. a 3 . 2 a 3 3 = a 3
Vậy V 3 + V a 3 - 1 = a
Đáp án B
Đáp án D
Gọi M là giao điểm của AI và BC; gọi N là giao điểm của A'J và B'C'. Suy ra M,N lần lượt là trung điểm của BC,B'C'.
Ta có M N / / B B ' A A ' / / B B ' ⇒ M N / / A A ' . Mặt khác M N = B B ' ⇒ M N = A A ' .
Từ hai dữ kiện trên suy ra AMNA' là hình bình hành. Vậy thiết diện tạo bởi mặt phẳng (ẠIJ) và hình lăng trụ là hình bình hành.