Giá trị của tổng 4 + 44 + 444 + . . . + 4 . . . 4 (tổng đó có 2018 số hạng) bằng
A. 4 9 10 2019 - 10 9 - 2018
B. 4 9 10 2019 - 10 9 + 2018
C. 4 9 10 2018 - 1
D. 40 9 10 2018 - 1 + 2018
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

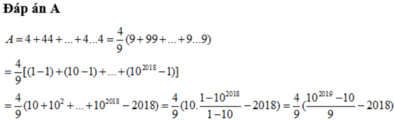

Đáp án D
Lời giải:
A = 4 9 9 + 99 + ... + 99...9 = 4 9 1 − 1 + 10 − 1 + 10 2 − 1 + .... + 10 2018 − 1 = 4 9 1 + 10 + 10 2 + ... + 10 2018 − 2019 = 4 9 10 2019 − 1 10 − 1 − 2019 = 4 9 10 2019 − 10 9 − 2018

Lời giải:
Đặt \(\underbrace{11...1}_{n}=a\Rightarrow 9a+1=10^n\Rightarrow a=\frac{10^n-1}{9}\Rightarrow \underbrace{44...4}_{n}=4a=\frac{4}{9}(10^n-1)\)
Thay $n=1,2,...,2018$ và đặt tổng cần tính là $T$
Khi đó:
\(T=\frac{4}{9}(10^1-1)+\frac{4}{9}(10^2-1)+\frac{4}{9}(10^3-1)+...+\frac{4}{9}(10^{2018}-1)\)
\(=\frac{4}{9}(10+10^2+10^3+...+10^{2018}-2018)\)
\(10T=\frac{4}{9}(10^2+10^3+...+10^{2019}-20180)\)
Trừ theo vế:
\(9T=10T-T=\frac{4}{9}(10^{2019}-20180-10+2018)=\frac{4}{9}(10^{2019}-18172)\)
\(\Rightarrow T=\frac{4(10^{2019}-18172)}{81}\)


Bài 1 :
Gọi số nữ và số nam thuận tay trái lần lượt là x(người) và y(người).
Khi đó, do tổng số người thuận tay trái là 10 người nên ta có
x+y=10
Lại có số nữ thuận tay phải gấp 3 lần số nữ thuận tay trái nên số nữ thuận tay phải là 3x(người). Số nam thuận tay phải gấp 5 lần số nam thuận tay trái nên số nam thuận tay phải là 5y(người).
Lại có tổng số người thuận tay phải là 44 nên ta có :
\(3x+5y=44\)
Vậy ta có hệ
\(\hept{\begin{cases}x+y=10\\3x+5y=44\end{cases}}\)
Suy ra \(x=3,y=7\)
Vậy có 3 nữ thuận tay trái, 7 nam thuận tay trái.
Bài 2 :
\(\hept{\begin{cases}a^2+b^2+c^2=27\left(1\right)\\a+b+c=9\left(2\right)\end{cases}}\)
Áp dụng bất đẳng thức Cô si ta có :
\(2\left(a^2+b^2+c^2\right)=\left(a^2+b^2\right)+\left(b^2+c^2\right)+\left(c^2+a^2\right)\)
\(\ge2ab+2bc+2ca\)
\(\Rightarrow a^2+b^2+c^2\ge ab+bc+ca\)
Dấu " = " xảy ra <=> a=b=c
\(\left(2\right)\Leftrightarrow\left(a+b+c\right)^2=81\)
\(\Leftrightarrow a^2+b^2+c^2+2ab+2bc+2ca=81\)
\(\Rightarrow81\le a^2+b^2+c^2+2\left(a^2+b^2+c^2\right)=3\left(a^2+b^2+c^2\right)\)
\(\Rightarrow27\le a^2+b^2+c^2\left(3\right)\)
Từ (1) và (3) => dấu " = " xảy ra => a=b=c=3
\(\Rightarrow B=\left(3-4\right)^{2018}+\left(3-4\right)^{2019}+\left(3-4\right)^{2020}\)
\(=1-1+1=1\)

Tớ hướng dẫn câu A thui, mấy câu còn lại làm tương tự
A = 9 + 99 + 999 + ... + 99...9(10 chữ số 9)
Ta để ý: 9 = 101 - 1
99 = 102 - 1
999 = 103 - 1
.....
99..9(10 chữ số 9) = 1010 - 1
Công thức tổng quát: \(\overline{aa...aa}=\frac{a}{9}\left(10^n-1\right)\) với n là số chữ số của aa..aa
Suy ra tổng A = 101 + 102 + 103 + ... + 1010 - 10
=> A = 11111111110 - 10 = 111111111100
B,C làm tương tự với công thức tổng quát