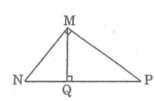
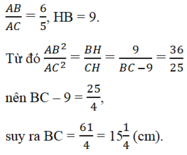Đường cao MQ của tam giác vuông MNP chia cạnh huyển NP thành hai đoạn NQ = 3, PQ = 6. Hãy so sánh cotg ∠ N và cotg ∠ P . Tỉ số nào lớn hơn và lớn hơn bao nhiêu lần?
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
16 tháng 9 2017
Đúng(0)
Những câu hỏi liên quan
HH
16 tháng 7 2020
Trong tam giác MNQ vuông tại Q , ta có :
\(cotg \widehat{N}=\frac{NQ}{MQ}=\frac{3}{MQ}\)
Tam giác MPQ vuông tại Q , ta có :
\(cotg \widehat{P} =\frac{PQ}{MQ}=\frac{6}{MQ}\)
Ta có : \(\frac{6}{MQ}>\frac{3}{MQ}\)nên \(cotg \widehat{P } > cotg \widehat{N}\)
\(\frac{cotg \widehat{P}}{cotg \widehat{N}}=\frac{\frac{6}{MQ}}{\frac{3}{MQ}}=\frac{6}{MQ}.\frac{MQ}{3}=\frac{6}{3}=2\)
Vậy : \(cotg \widehat{P} =2cotg \widehat{N}\)
12 tháng 2 2022
\(MQ=\sqrt{3\cdot6}=3\sqrt{2}\left(cm\right)\)
\(\cot N=\dfrac{NQ}{MQ}=\dfrac{3}{3\sqrt{2}}=\dfrac{1}{\sqrt{2}}\)
\(\cot P=\dfrac{MQ}{PQ}=\dfrac{3\sqrt{2}}{6}=\dfrac{\sqrt{2}}{2}\)
Do đó: \(\cot N=\cot P\)
1 tháng 7 2017
Hình bạn tự vẽ
Ta có :NP= NQ+PQ=3+6=9
Áp dụng hệ thức giữa cạnh và đường cao vào tam giác MNP vuông tại M ta có:
\(MN=\sqrt{NP.MN}=\sqrt{9.3}=3\sqrt{3}\)
TT ta có MP=\(3\sqrt{6}\)
Từ đó suy ra cot N và cot P rồi tự tính
VT
1 tháng 7 2017
@@ phần này mk làm r... ko biết so sánh như nào thôi...
cotN = \(\dfrac{MN}{MP}\) = \(\dfrac{3\sqrt{3}}{3\sqrt{6}}\) = \(\dfrac{\sqrt{3}}{\sqrt{6}}\) = \(\dfrac{1}{\sqrt{2}}\)
cotP = \(\dfrac{MP}{MN}\) = \(\dfrac{3\sqrt{6}}{3\sqrt{3}}\) = \(\sqrt{2}\)
như này rồi so sánh sao....
CM
18 tháng 8 2019
Giả sử tam giác ABC có góc (BAC) = 90 °
Theo đề bài, ta có: BC – AB = 1 (cm) (1)
AB + AC – BC = 4 (cm) (2)
Từ (1) và (2) suy ra: BC – AB + AB + AC – BC = 4 + 1 = 5 (cm)
Theo định lí Pi-ta-go, ta có: B C 2 = A B 2 + A C 2 (3)
Từ (1) suy ra: BC = AB + 1 (4)
Thay (4) vào (3) ta có:
A B 2 + 1 2 = A B 2 + A C 2
⇔ A B 2 + 2 A B + 1 = A B 2 + 5 2
⇔ 2AB = 24 ⇔ AB = 12 (cm)
Thay AB = 12 (cm) vào (1) ta có: BC = 12 + 1 = 13 (cm)
CM
17 tháng 3 2017
Xét tam giác ABC vuông tại A với AB > AC, gọi AH là đường cao kẻ từ A thì ta có:
