Tìm x biết:
b) 60%x = 90
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
12 tháng 1 2018
Đúng(0)
Những câu hỏi liên quan
27 tháng 7 2021
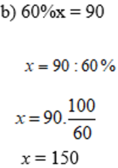
\(\Leftrightarrow\dfrac{1}{2}x+\dfrac{2}{3}x-x=-4\Leftrightarrow\dfrac{3x+4x-6x}{6}=-\dfrac{24}{6}\)
\(\Rightarrow x=-24\)
C0
2
28 tháng 11 2021
b) 50-3(x+4)=14
3(x+4)=36
x+4=13
x=9
c)2⁸‐ⁿ+75=107
2⁸-ⁿ=32
2⁸-ⁿ=2⁵
8-x=5
x=3
MT
6
7 tháng 9 2021
\(2x\left(x+3\right)-3\left(x^2+1\right)=x+1-x\left(x-2\right)\)
\(\Leftrightarrow2x^2+6x-3x^2-3=x+1-x^2+2x\)
\(\Leftrightarrow-x^2+6x-3=-x^2+3x+1\)
\(\Leftrightarrow3x=4\)
hay \(x=\dfrac{4}{3}\)
NT
7 tháng 9 2021
\(2x\left(x+3\right)-3\left(x^2+1\right)=x+1-x\left(x-2\right)\)
\(\Leftrightarrow2x^2+6x-3x^2-3=x+1-x^2+2x\)
\(\Leftrightarrow3x=4\Leftrightarrow x=\dfrac{4}{3}\)
13 tháng 1 2018
b ) - 25 + ( - 16 + x ) = 0
( - 16 + x ) = 0 - ( - 25 )
- 16 + x = 25
x = 25 - ( - 16 )
x = 41
Vậy x = 41
21 tháng 10 2021
\(B=\overline{2x10y9}⋮9\left(0\le x,y\le9\right)\)
\(\Rightarrow\left(2+x+1+0+y+9\right)⋮9\)
\(\Rightarrow\left(12+x+y\right)⋮9\)
Do \(0\le x,y\le9\)
\(\Rightarrow\left[{}\begin{matrix}x+y=6\\x+y=15\end{matrix}\right.\)
\(\Rightarrow\left(x;y\right)\in\left\{\left(1;5\right),\left(5;1\right),\left(2;4\right),\left(4;2\right),\left(3;3\right),\left(6;9\right),\left(9;6\right),\left(8;7\right),\left(7;8\right)\right\}\)
NH
2
K
10 tháng 12 2021
\(35-5\left(x-1\right)=10\\ \Leftrightarrow35-5x+5=10\\ \Rightarrow40-5x=10\)
\(\Rightarrow-5x=10-40\\ \Rightarrow-5x=-30\\ \Rightarrow x=\dfrac{-30}{-5}=6\)
c)
\(24\left(x-16\right)=12^2\)
\(\Rightarrow24x-384=144\\ \Rightarrow24x=144+384\\ \Rightarrow24x=528\\ \Rightarrow x=\dfrac{528}{24}=22\)
d)
\(\left(x^2-10\right)\div5=3\\ \Rightarrow\left(x^2-10\right)=3\times5\\ \Rightarrow x^2-10=15\)
\(\Rightarrow x^2=15+10\\ \Rightarrow x^2=25\\ \Rightarrow x^2=5^2\Rightarrow x=5\)
13 tháng 2 2018
Ta có :
\(\left|3x+18\right|\ge0\) và \(\left|4x-28\right|\ge0\) \(\Rightarrow\) \(\left|3x+18\right|+\left|4y-28\right|\ge0\)
Mà \(\left|3x+18\right|+\left|4y-28\right|\le0\) ( đề bài cho )
\(\Rightarrow\)\(\left|3x+18\right|+\left|4y-28\right|=0\)
\(\Leftrightarrow\)\(\orbr{\begin{cases}3x+18=0\\4y-28=0\end{cases}\Leftrightarrow\orbr{\begin{cases}3x=-18\\4y=28\end{cases}\Leftrightarrow}\orbr{\begin{cases}x=-6\\y=7\end{cases}}}\)
Vậy \(x=-6\) và \(y=7\)
13 tháng 2 2018
Ta có \(\left|3x+18\right|+\left|4y-28\right|\le0\)
Mà \(\left|3x+18\right|\ge0\forall x;\left|4y-28\right|\ge0\forall y\)
=> |3x+18|+|4y-28|=0
=> 3x+18=4y-28=0
• 3x+18=0 <=> 3x=-18 <=> x=-6
• 4y-28=0 <=> 4y=28 <=> y=7
Vậy ...
9 tháng 5 2022
`4x^2 = 13`.
`=> x^2 = 13/4`.
`=> x = (sqrt 13)/(sqrt 4)`
`=> x = (+-sqrt 13)/2`.
Vậy `S = (+-sqrt 13)/2`.