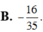
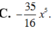
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
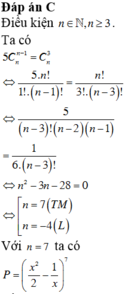
Đáp án C
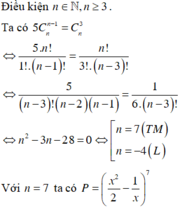
Số hạng thứ k + 1 trong khai triển T k + 1 = − 1 k 2 7 − k . C 7 k . x 14 − 3 k
Suy ra 14 − 3 k = 5 ⇔ k = 3
Vậy số hạng chứa x 5 trong khai triển là T 4 = − 35 16 x 5 .
`2^n C_n ^0+2^[n-1] C_n ^1+2^[n-2] +... +C_n ^n=59049`
`<=>(2+1)^n=59049`
`<=>3^n=59049`
`<=>n=10 =>(2x^2+1/[x^3])^10`
Xét số hạng thứ `k+1:`
`C_10 ^k (2x^2)^[10-k] (1/[x^3])^k ,0 <= k <= 10`
`=C_10 ^k 2^[10-k] x^[20-5k]`
Số hạng chứa `x_5` xảy ra `<=>20-5k=5<=>k=3`
Với `k=3` thì số hạng cần tìm là: `C_10 ^3 2^[10-3] x^5=15360 x^5`
Điều kiện: 2 ≤ n ∈ N
Ta có
A n + 3 3 - 6 C n + 1 3 = 294 ⇔ n + 3 ! n ! - 6 n + 1 ! 3 ! n - 2 ! = 294 ⇔ n + 3 n + 2 n + 1 - n + 1 n n - 1 = 294 ⇔ n 2 + 2 n - 48 = 0 ⇔ n = 6 n = - 8
So với điều kiện chọn n = 6
Với n = 6 ta có 2 x 4 y + y 2 x 2 6 = ∑ k = 0 6 C 0 k 2 x 4 y 6 - k y 2 x 2 k = ∑ k = 0 6 C 0 k 2 6 - k x 24 - 6 k y - 6 + 3 k
Giả thiết bài toán cho ta 24 - 6 k - 6 + 3 k = 18 ⇔ k - 3 2 = 0 ⇔ k = 3
Khi k = 3 ta thu được số hạng thỏa mãn yêu cầu bài toán là: C 6 3 2 2 x 6 y 3 = 160 x 6 y 3
Đáp án D
Đáp án D
Ta có: ( x − 2 x 2 ) 21 = ∑ k = 0 21 C 21 k . x k . ( − 2 x 2 ) 21 − k = ∑ k = 0 21 C 21 k . x k − 2 ( 21 − k ) ( − 2 ) 21 − k
Số hạng không chứa x ó k – 2(21 – k) = 0 ó k = 14
Số cần tìm là C 21 14 ( − 2 ) 21 − 14 = C 21 7 ( − 2 ) 7 (theo tính chất C n k = C n n − k )
