Tìm tất cả các giá trị thực của tham số
α
và
β
sao cho hàm số 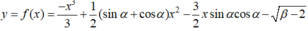
luôn giảm trên ℝ ?

![]()

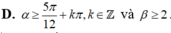
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Điều kiện xác định: β ≥ 2
Yêu cầu của bài toán đưa đến giải bất phương trình 1 2 ≤ sin 2 α ≤ 1
Kết luận: π 12 + k π ≤ α ≤ 5 π 12 + kπ , k ∈ ℤ và β ≥ 2
Chọn B.

Đáp án C.
Dễ thấy hàm số liên tục trên các khoảng 0 ; + ∞ và - ∞ ; 0 . Ta có:
f 0 = - m lim x → 0 + f x = - m lim x → 0 - f ( x ) = 2 . Để hàm số liên tục tại x = 0 thì lim x → 0 + f x = lim x → 0 - f x = f 0 ⇔ m = - 2 .