Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
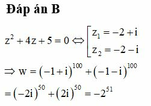
Phương trình: \(z^2+4z+5=0\)
có 2 nghiệm: \(\left\{{}\begin{matrix}z_1=-2+i\\z_2=-2-i\end{matrix}\right.\)
+) \(\left(1+z_1\right)^{100}=\left(\left(-1+i\right)^2\right)^{50}\\ =\left(-2i\right)^{50}=\left(\left(-2i\right)^2\right)^{25}=\left(-4\right)^{25}=-2^{50}\)
+) \(\left(1+z_2\right)^{100}=\left(\left(-1-i\right)^2\right)^{50}\\ =\left(2i\right)^{50}=\left(\left(2i\right)^2\right)^{25}=\left(-4\right)^{25}=-2^{50}\)
Vậy: \(w=-2^{50}-2^{50}=-2^{51}\)
Chọn C.
Không mất tính tổng quát ta gọi 4 nghiệm của phương trình là:
z1= 1; z2= - 2; z3= 1+ i và z4 = 1 - i
Thay vào biểu thức
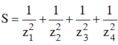
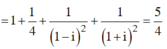
Đáp án A
Phương pháp.
Giả sử 
Giả phương trình ban đầu để tìm được nghiệm
z
1
,
z
2
Sử dụng giả thiết để đánh giá cho cho b. Đưa 
về một hàm cho b và sử dụng ước lượng cho b ở phần trước để tìm giá trị nhỏ nhất của P.
Lời giải chi tiết.
Tính toán ta tìm được hai nghiệm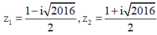 
Giả sử 
. Từ 
ta suy ra
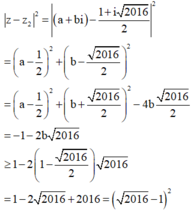
Áp dụng (1) ta nhận được
Do đó giá trị nhỏ nhất của 
là
2016
-
1
Đạt được khi và chỉ khi 
Đáp án A
Phương trình z 2 − z + 2017 2 = 0 ⇔ 4 z 2 − 4 z + 2017 = 0
⇔ 2 z − 1 2 = 2016 i 2 ⇔ z 1 = 1 − i 2016 2 z 2 = 1 + i 2016 2
Ta có z − z 1 + z − z 2 ≥ z − z 1 − z − z 2 = z − z 2 ≥ z 1 − z 2 − z − z 1 = 2016 − 1
Vật giá trị nhỏ nhất của biểu thức P là P min = 2016 − 1
