Cho đồ thị hàm số đạt cực đại tại và đạt cực tiểu tại . Tính giá trị của biểu thức
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án C.
Xét hàm số y = a x 4 + b x 2 + c , ta có y ' = 4 a x 3 + 2 b x ; y ' ' = 12 a x 2 + 2 b ; ∀ x ∈ ℝ .
Điểm A(0;-2) là điểm cực đại của đồ thị hàm số ⇒ y ' 0 = 0 ⇔ y 0 = - 2 y ' ' 0 < 0 ⇔ c = - 2 b > 0 .
Điểm B( 1 2 ; - 17 8 ) là điểm cực tiểu của đồ thị hàm số ⇒ y ' 1 2 = 0 ; y 1 2 = - 17 8 y ' ' 0 > 0
⇔ a 2 + b = 0 a 16 + b 4 + c = - 17 8 ⇔ a + 2 b = 0 a + 4 b = - 2 ⇔ a = 2 b = - 1 ⇒ a + b + c = - 1 .

a.
\(\left\{{}\begin{matrix}-\dfrac{b}{2a}=-2\\4a-2b+c=4\\c=6\end{matrix}\right.\) \(\Rightarrow\left\{{}\begin{matrix}b=4a\\4a-2.4a+6=4\\c=6\end{matrix}\right.\)
\(\Rightarrow\left\{{}\begin{matrix}b=4a=2\\a=\dfrac{1}{2}\\c=6\end{matrix}\right.\) \(\Rightarrow y=\dfrac{1}{2}x^2+2x+6\)
b.
\(y_{min}=y_{CT}=\dfrac{4ac-b^2}{4a}=\dfrac{4.1.1-\left(-4\right)^2}{4.1}=-3\)

Đáp án C.
Xét hàm số y = a x 4 + b x 2 + c ,
ta có y ' = 4 a x 3 + 2 b x ; ∀ x ∈ ℝ .
Điểm A 0 ; − 2 là điểm cực trị đại của đồ thị hàm số ⇒ y 0 = − 2 y ' 0 = 0 ⇔ c = − 2
Điểm B 1 2 ; − 17 8 là điểm cực tiểu của đồ thị hàm số ⇒ y 1 2 = − 17 8 y ' 1 2 = 0 ⇔ a 2 + b = 0 a 16 + b 4 = − 1 8
Từ đó suy ra a = 2 ; b = − 1 ; c = − 2 ⇒ tổng a + b + c = − 1.

Phương pháp:
Quan sát đồ thị hàm số đã cho để kết luận.
Cách giải:
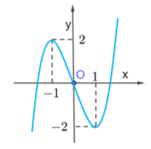
Dựa vào đồ thị hàm số đã cho ta thấy hàm số đã cho đạt cực đại tại x=-1
Chọn A.

1.
\(y'=4x^3-4\left(m+1\right)x\)
\(y''=12x-4\left(m+1\right)\)
Hàm đạt cực đại tại x=1 khi: \(\left\{{}\begin{matrix}y'\left(1\right)=0\\y''\left(1\right)< 0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}4-4\left(m+1\right)=0\\12-4\left(m+1\right)< 0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}m=0\\m>2\end{matrix}\right.\)
Không tồn tại m thỏa mãn
2.
\(y'=4x^3-2\left(m+1\right)x\)
\(y''=12x^2-2\left(m+1\right)\)
Hàm đạt cực tiểu tại x=-1 khi:
\(\left\{{}\begin{matrix}y'\left(-1\right)=0\\y''\left(-1\right)>0\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}-4+2\left(m+1\right)=0\\12-2\left(m+1\right)>0\end{matrix}\right.\)
\(\Leftrightarrow\left\{{}\begin{matrix}m=1\\m< 5\end{matrix}\right.\) \(\Rightarrow m=1\)


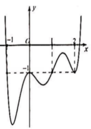
Hình ảnh trên là một phần đồ thị của y trên tập xác định. Ta thấy rằng hàm số đạt cực đại tại x = 2 nhưng không chắc rằng có còn điểm cực đại nào khác trên những khoảng rộng hơn hay không (I) sai, (III) đúng.
Hàm số không xác định tại x = 1 nên không thể đạt cực tiểu tại điểm này =>(II) sai.
Chọn B

Đáp án D
Hàm số y = f ( x ) đạt cực tiểu tại x 0 = 0
Hàm số y = f ( x ) có ba điểm cực trị.
Phương trình f ( x ) = 0 có 4 nghiệm phân biệt
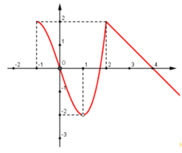
Hàm số đạt giá trị nhỏ nhất là -2 trên đoạn [-2;2]
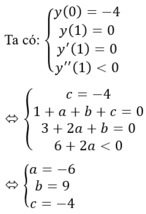



Đáp án B
TXĐ: D = R
Đạo hàm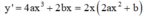
Điều kiện để hàm số có cực đại và cực tiểu là ab < 0
Hàm số đạt cực đại tại A(0;3) ⇔ c = 3
Hàm số đạt cực tiểu tại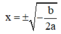 và điểm cực tiểu là B(1;-3), suy ra
và điểm cực tiểu là B(1;-3), suy ra