Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Ta có 64 = -8a + 4b - 2c + d; -61 = 27a + 9b + 3c +d
Từ y ' = 3 a x 2 + 2 b x + c ta thu được hai phương trình 0 = 12a - 4b + c; 0 = 27a + 6b + c
Giải hệ gồm 4 phương trình trên ta thu được a = 2; b = -3; c = -36; d = 20 hay a + b + c + d = -17
Đáp án C
Đáp án C.
Xét hàm số y = a x 4 + b x 2 + c , ta có y ' = 4 a x 3 + 2 b x ; y ' ' = 12 a x 2 + 2 b ; ∀ x ∈ ℝ .
Điểm A(0;-2) là điểm cực đại của đồ thị hàm số ⇒ y ' 0 = 0 ⇔ y 0 = - 2 y ' ' 0 < 0 ⇔ c = - 2 b > 0 .
Điểm B( 1 2 ; - 17 8 ) là điểm cực tiểu của đồ thị hàm số ⇒ y ' 1 2 = 0 ; y 1 2 = - 17 8 y ' ' 0 > 0
⇔ a 2 + b = 0 a 16 + b 4 + c = - 17 8 ⇔ a + 2 b = 0 a + 4 b = - 2 ⇔ a = 2 b = - 1 ⇒ a + b + c = - 1 .
Đáp án A
Hàm số f(x) xác định trên D⊆ R
Điểm
x
0
∈ D được gọi là điểm cực đại của hàm số f(x) nếu tồn tại một khoảng (a;b)⊂ D sao cho
x
0
∈ (a;b) và f(
x
0
)>f(x),∀x ∈ (a,b)∖{
x
0
}.
Đáp án A
Hàm số f(x) xác định trên D⊆ R
Điểm xo∈ D được gọi là điểm cực đại của hàm số f(x) nếu tồn tại một khoảng (a;b)⊂ D sao cho xo∈ (a;b) và f(xo)>f(x),∀x ∈ (a,b)∖{xo}.
Đáp án C.
Xét hàm số y = a x 4 + b x 2 + c ,
ta có y ' = 4 a x 3 + 2 b x ; ∀ x ∈ ℝ .
Điểm A 0 ; − 2 là điểm cực trị đại của đồ thị hàm số ⇒ y 0 = − 2 y ' 0 = 0 ⇔ c = − 2
Điểm B 1 2 ; − 17 8 là điểm cực tiểu của đồ thị hàm số ⇒ y 1 2 = − 17 8 y ' 1 2 = 0 ⇔ a 2 + b = 0 a 16 + b 4 = − 1 8
Từ đó suy ra a = 2 ; b = − 1 ; c = − 2 ⇒ tổng a + b + c = − 1.
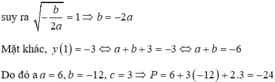
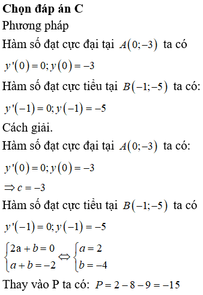
Đáp án B
TXĐ: D = R
Đạo hàm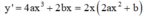
Điều kiện để hàm số có cực đại và cực tiểu là ab < 0
Hàm số đạt cực đại tại A(0;3) ⇔ c = 3
Hàm số đạt cực tiểu tại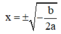
và điểm cực tiểu là B(1;-3), suy ra