Có bao nhiêu giá trị nguyên của tham số a thuộc đoạn [0

PT

Pham Trong Bach

9 tháng 6 2019

Có bao nhiêu giá trị nguyên của tham số a thuộc đoạn [0;2018] sao cho ba số 5 x + 1 + 5 1 - x , a 2 , 25 x + 25 - x theo thứ tự đó, lập thành một cấp số cộng? A. 2007. B. 2018. C. 2006. D....

Đọc tiếp

#Toán lớp 12

1

CM

Cao Minh Tâm

9 tháng 6 2019

Đúng(0)

PT

Pham Trong Bach

9 tháng 9 2017

Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [−10; 10] để phương trình m x 2 - m x + 1 = 0 có nghiệm.

A. 17

B. 18

C. 20

D. 21

#Toán lớp 10

1

CM

Cao Minh Tâm

9 tháng 9 2017

Nếu m = 0 thì phương trình trở thành 1 = 0 : vô nghiệm.

Khi m ≠ 0 , phương trình đã cho có nghiệm khi và chỉ khi

∆ = m 2 - 4 m ≥ 0 ⇔ m ≤ 0 m ≥ 4

Kết hợp điều kiện m ≠ 0 , ta được m < 0 m ≥ 4

Mà m ∈ Z và m ∈ [−10; 10] ⇒ m ∈ {−10; −9; −8;...; −1} ∪ {4; 5; 6;...; 10}.

Vậy có tất cả 17 giá trị nguyên m thỏa mãn bài toán.

Đáp án cần chọn là: A

Đúng(0)

PT

Pham Trong Bach

11 tháng 3 2019

Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn − 15 ; 5 để phương trình 4 x + m 2 x + 2 m − 4 = 0 có nghiệm?

A. 18.

B. 17.

C. 20.

D. 19.

#Mẫu giáo

1

CM

Cao Minh Tâm

11 tháng 3 2019

+) Phương trình ban đầu có nghiệm khi và chỉ khi phương trình bậc hai ẩn t có nghiệm dương.

Cách giải:

Đúng(0)

PT

Pham Trong Bach

6 tháng 5 2017

Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-2017;2018] để hàm số y = 1 3 x 3 - m x 2 + ( m + 2 ) x có hai điểm cực trị nằm trong khoảng 0 ; + ∞ . A. 2015 B. 2016 C. 2018 D....

Đọc tiếp

#Mẫu giáo

1

CM

Cao Minh Tâm

6 tháng 5 2017

Đúng(0)

PT

Pham Trong Bach

1 tháng 8 2018

Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-2017;2018] để hàm số y = 1 3 x 3 - m x 2 + ( m + 2 ) x có hai điểm cực trị nằm trong khoảng 0 ; + ∞ .

A. 2015

B. 2016

C. 2018

D. 4035

#Toán lớp 12

1

CM

Cao Minh Tâm

1 tháng 8 2018

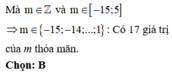
Chọn B

Phương pháp:

Từ ycbt suy ra ta phải tìm m để hàm số có hai điểm cực trị dương hay phương trình y' = 0 có hai nghiệm dương phân biệt.

Ta sử dụng phương trình có hai nghiệm dương phân biệt

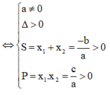
Cách giải:

Ta có

Từ ycbt suy ra ta phải tìm m để hàm số có hai điểm cực trị dương hay phương trình y' = 0 có hai nghiệm dương phân biệt.

Khi đó

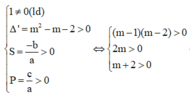
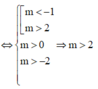
Mà nên có 2018 – 3 + 1 = 2016 giá trị m thỏa mãn.

Đúng(0)

PT

Pham Trong Bach

28 tháng 6 2019

Có bao nhiêu giá trị nguyên thuộc đoạn [0;2019] của tham số m để phương trình 4 x - m + 2018 2 x + 2019 + 3 m = 0 có hai nghiệm trái dấu?

A.2016

B.2019

C.2013

D.2018

#Toán lớp 12

1

CM

Cao Minh Tâm

28 tháng 6 2019

Chọn B

Đúng(0)

PT

Pham Trong Bach

20 tháng 10 2018

Có tất cả bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-3; 3] để phương trình ( m 2 + 2 ) c o s 2 x - 2 m sin 2 x + 1 = 0 có nghiệm

A. 3

B. 7

C. 6

D. 4

#Mẫu giáo

1

CM

Cao Minh Tâm

20 tháng 10 2018

Đúng(0)

PT

Pham Trong Bach

10 tháng 6 2019

Hỏi có bao nhiêu giá trị nguyên của tham số thực m để phương trình logarit log 3 2 x + log 3 2 x + 1 - 2 m - 1 = 0 có nghiệm thuộc đoạn 1 ; 3 3 A. 3 B. 2 C. 1...

Đọc tiếp

#Toán lớp 12

1

CM

Cao Minh Tâm

10 tháng 6 2019

Chọn A.

Đặt . Với suy ra 1 ≤ t ≤ 2.

Phương trình đã cho trở thành t²+ t = 2m + 2 (*)

Phương trình đã cho có nghiệm thuộc đoạn có nghiệm 1 ≤ t ≤ 2

Xét hàm số f(t) = t²+ t với1 ≤ t ≤ 2 , ta thấy f’(t) = 2t + 1 nên f(t) là hàm đồng biến trên đoạn [1; 2]

Suy ra 2 = f(1) ≤ f(t) ≤ f(2) = 6

Vậy phương trình có nghiệm khi 2 ≤ 2m + 2 ≤ 6 hay 0 ≤ m ≤ 2

Suy ra có 3 giá trị nguyên m thỏa mãn yêu cầu bài toán.

Đúng(0)

PT

Pham Trong Bach

17 tháng 7 2017

Có bao nhiêu giá trị nguyên của tham số thực m thuộc đoạn − 2018 ; 2018 để hàm số f x = x + 1 ln x + 2 − m x đồng biến trên khoảng 0 ; e 2 A. 2014 B. 2023 C. 2016 D....

Đọc tiếp

#Mẫu giáo

1

CM

Cao Minh Tâm

17 tháng 7 2017

Đúng(0)

PT

Pham Trong Bach

13 tháng 8 2017

Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn [-20;20] để bất phương trình 2 2 x + 1 - 12 m . 2 x - 1 + 5 m 2 - 10 < 0 có nghiệm thực? ...

Đọc tiếp

#Toán lớp 12

1

CM

Cao Minh Tâm

13 tháng 8 2017

Đúng(0)

PT

Pham Trong Bach

30 tháng 10 2018

Có bao nhiêu giá trị nguyên của tham số m thuộc đoạn - 20 ; 20 để bất phương trình 2 2 x + 1 - 12 m . 2 x - 1 + 5 m 2 - 10 < 0 có nghiệm thực? A. 38 B. 3 C. 6. D....

Đọc tiếp

#Mẫu giáo

1

CM

Cao Minh Tâm

30 tháng 10 2018

Đúng(0)

Chúng tôi đề xuất

Tài nguyên

Ứng dụng mobile

Bảng xếp hạng

Các khóa học có thể bạn quan tâm

Yêu cầu VIP