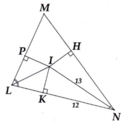
Cho hình vẽ bên, biết KN = 12 cm, IN = 13 cm và I là giao điểm, các phân giác của tam giác MNL.
a) So sánh IP và IH.
b) Tính IH.
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
H9
HT.Phong (9A5)
CTVHS
5 tháng 4 2023
a) Vì I là giao điểm của các đường phân giác của \(\Delta MNP\) nên nó cách đều các cạnh của \(\Delta MNP\)
\(\Rightarrow IH=IP\)
b) \(\Delta IKN\) vuông tại K áp dụng định lý Pi-ta-go ta có:
\(IN^2=IK^2+KN^2\)
\(\Rightarrow IK^2=IN^2-KN^2\)
\(\Rightarrow IK^2=13^2-12^2\)
\(\Rightarrow IK^2=25\)
\(\Rightarrow IK=\sqrt{25}=5\left(cm\right)\)
Vì I cách đều các cạnh của \(\Delta MNP\) nên
\(\Rightarrow IK=IH=5\left(cm\right)\)
27 tháng 1 2022
a: Xét ΔBAI vuông tại A và ΔBHI vuông tại H có
BI chung
\(\widehat{ABI}=\widehat{HBI}\)
Do đó: ΔBAI=ΔBHI
Suy ra: IA=IH
b: Xét ΔAIK vuông tại A và ΔHIC vuông tại H có
IA=IH
\(\widehat{AIK}=\widehat{HIC}\)
Do đó: ΔAIK=ΔHIC
Suy ra: IK=IC
hay ΔIKC cân tại I
5 tháng 5 2022
Trong tam giác ABC có:
∠A + ∠(ABC) + ∠(ACB) = 180o ⇒ ∠(ABC) + ∠(ACB) = 180o - 80o = 100o
Mà BI và CI lâ các tia phân giác nên
∠(ABC) + ∠(ACB) = 2.∠(IBC) + 2.∠(ICB) = 2 (∠(IBC) + ∠(ICB) )
Suy ra ∠(IBC) + ∠(ICB) = 50o
Mà ∠(IBC) + ∠(ICB) + ∠(BIC) = 180o ⇒ ∠(BIC) = 130o.
RM
12 tháng 6
Bài giải :
a, SAMC = SABM ( vì MC = MB ) và có chung chiều cao hạ từ A xuống đáy CB
Vậy tỉ số chiều cao MQ/MP = = AC/AB =
Vậy AC gấp 2 lần AB
b, Diện tích tam giác ABC là :
21 × 2 = 42
Đáp số : ......................
25 tháng 8 2018
câu a bài 2 nhá
a) Gọi D là trung điểm BI => góc IDM = 45 độ
DM // IC ( đường trung bình )
=> góc BIC = 135 độ
=> 180 -1/2( góc B + góc C ) =135 độ
=> góc B + góc C = 90 độ
=> góc A = 90 độ
13 tháng 2 2022
a: \(BH=\sqrt{AB^2-AH^2}=5\left(cm\right)\)
\(AC=\sqrt{AH^2+HC^2}=20\left(cm\right)\)
BC=BH+CH=21(cm)
Chu vi tam giác ABC là:
\(C=20+21+13=54\left(cm\right)\)
b: Xét ΔABC có AB<AC<BC
nên \(\widehat{C}< \widehat{B}< \widehat{A}\)
h