Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


(Bạn tự vẽ hình giùm)
a/ Ta có \(\Delta ABC\)vuông tại A
=> BC2 = AB2 + AC2 (định lý Pitago)
=> BC2 = 62 + 82
=> BC2 = 36 + 64
=> BC2 = 100
=> \(BC=\sqrt{100}=10\)(cm)
b/ \(\Delta ABI\)vuông và \(\Delta HBI\)vuông có: \(\widehat{ABI}=\widehat{HBI}\)(BI là tia phân giác của \(\widehat{ABC}\))
Cạnh BI chung
=> \(\Delta ABI\)vuông = \(\Delta HBI\)vuông (ch - gn) (đpcm)
c/ Ta có \(\Delta ABI\)= \(\Delta HBI\)(cmt) => \(\hept{\begin{cases}BA=BH\\IA=IH\end{cases}}\)(hai cặp cạnh tương ứng)
=> BI cách đều hai đầu đoạn thẳng AH
=> BI là đường trung trực của AH (đpcm)
d/ \(\Delta IHC\)vuông tại H có: IH < IC (quan hệ giữa đường vuông góc và đường xiên)
và IA = IH (cm câu c)
=> IA < IC (đpcm)
e/ Mình xin chỉnh lại đề: CMR: I là trực tâm \(\Delta KBC\)
\(\Delta AIK\)và \(\Delta HIC\)có: \(\widehat{IAK}=\widehat{IHC}=90^o\)(vì AC \(\perp\)BK, KH \(\perp\)BC)
IA = IH (cm câu c)
\(\widehat{AIK}=\widehat{HIC}\)(đối đỉnh)
=> \(\Delta AIK\)= \(\Delta HIC\)(g. c. g) => AK = HC (hai cạnh tương ứng)
và AB = BH (cm câu c)
=> AK + AB = HC + BH
=> BK = BC
nên \(\Delta BKC\)cân tại B
=> Đường phân giác BI cũng là đường cao của \(\Delta BKC\)
=> BI \(\perp\)KC
Ta có: BI cắt KH tại I
Chứng minh:
Giả sử BI không cắt KH
=> BI // KH
Mà BI \(\perp\)KC (cmt)
=> KH \(\perp\)KC
và KH \(\perp\)BC (gt)
=> KC // BC
=> K, B, C thẳng hàng
Vô lý! (Vì K, B, C là ba đỉnh của một tam giác)
=> BI cắt KH tại I
=> I là trực tâm của \(\Delta KBC\)(đpcm)
Bài này lớp 7 nên mik ko biết làm.
Nhưng bạn thử zô Câu hỏi tương tự ik
Nhỡ đâu có .
Hok tốt nha Hoa

hic giúp mk đi xin lun đó !!!! zời ơi mấy người hok giỏi trong olm đâu zùi chán vãi !!!!
5665876978

a: Xét ΔAEH có
AI là đường cao
AI là đường trung tuyến
Do đó: ΔAEH cân tại A
hay AH=AE(1)
Xét ΔAFH có
AK là đường cao
AK là đường trung tuyến
Do đó: ΔAFH cân tại A
hay AH=AF(2)
Từ (1) và (2)suy ra AE=AF
b: \(\widehat{EAF}=2\cdot\left(\widehat{BAH}+\widehat{CAH}\right)=2\cdot60^0=120^0\)
nên \(\widehat{AEF}=\widehat{AFE}=30^0\)

M P N I H K
Câu a, b em tự làm nhé nó khá đơn giản
câu c)
Áp dụng định lí pitago cho 2 tam giác vuông IKM và IKP ta có:
\(IK^2=MI^2-MK^2\)
\(IK^2=IP^2-KP^2\)
Cộng vế theo vế ta có;
\(2IK^2=MI^2-MK^2+IP^2-KP^2=\left(MI^2+IP^2\right)-MK^2-KP^2=MP^2-MK^2-KP^2\)( Áp dụng định lí pita go cho tam giác MIP)
Mà MP=MN
=> Điều p cm

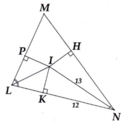
a) Vì I là giao điểm của các đường phân giác của \(\Delta MNP\) nên nó cách đều các cạnh của \(\Delta MNP\)
\(\Rightarrow IH=IP\)
b) \(\Delta IKN\) vuông tại K áp dụng định lý Pi-ta-go ta có:
\(IN^2=IK^2+KN^2\)
\(\Rightarrow IK^2=IN^2-KN^2\)
\(\Rightarrow IK^2=13^2-12^2\)
\(\Rightarrow IK^2=25\)
\(\Rightarrow IK=\sqrt{25}=5\left(cm\right)\)
Vì I cách đều các cạnh của \(\Delta MNP\) nên
\(\Rightarrow IK=IH=5\left(cm\right)\)

h