Cho phương trình 5 x + m = log 5 x - m với m là tham số. Có bao nhiêu giá trị nguyên của m ∈ - 20 ; 20 để phương trình đã cho có nghiệm?
A. 20.
B. 19.
C. 9.
D. 21.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

https://video.vietjack.com/upload2/quiz_source1/2020/01/100-bai-trac-nghiem-ham-so-mu-va-logarit-co-loi-giai-chi-tiet-3-1-1579254891.PNG
bạn tham khảo nha

Đáp án C.
Áp dụng bất đẳng thức Bunhiacopxki, ta có:
m . s inx+4cosx 2 ≤ m 2 + 4 2 sin 2 x + c os 2 x = m 2 + 16.
Nên để phương trình đã cho có nghiệm ⇔ 3 m − 5 2 ≤ m 2 + 16 ⇔ 3 m 2 20 m + 9 ≤ 0.
Kết hợp với m ∈ ℤ , ta được m = 1 ; 2 ; 3 ; 4 ; 5 ; 6 là giá trị cần tìm.

Chọn đáp án A
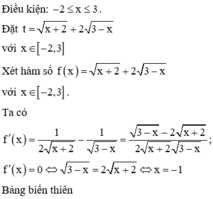

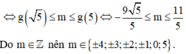
Vậy số giá trị nguyên của m để phương trình có nghiệm là 10.
Dựa vào bảng biến thiên ta có phương trình đã cho có nghiệm khi m ≤ - 0 , 92 .
Mặt khác m nguyên và m ∈ - 20 ; 20 vì vậy m = - 19 ; - 18 ; . . . ; - 1 nên có 19 giá trị m cần tìm.
Đáp án B.