Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Ta có \(\sqrt{\left(m+2\right)x+m}\ge\left|x-1\right|\Leftrightarrow\left(m+2\right)x+m\ge x^2-2x+1\)
\(\Leftrightarrow m\ge\frac{x^2-4x+1}{x+1}\) (vì \(x\in\left[0;2\right]\)
Xét hàm số \(f\left(x\right)=\frac{x^2-4x+1}{x+1}\) trên đoạn \(\left[0;2\right]\) ta có
\(f'\left(x\right)=\frac{x^2+2x-5}{\left(x+1\right)^2};f'\left(x\right)=0\Leftrightarrow x=-1+\sqrt{6}\)
Lập bảng biến thiên ta được
\(f\left(0\right)=1;f\left(2\right)=-1\)
\(f\left(-1+\sqrt{6}\right)=2\sqrt{6}-6\)
Vậy bất phương trình đã cho có nghiệm thì \(m>\) min (0;2] \(f\left(x\right)=f\left(-1+\sqrt{6}\right)=2\sqrt{6-6}\)


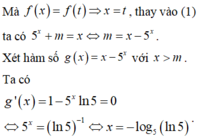
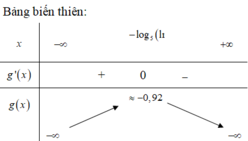
Dựa vào bảng biến thiên ta có phương trình đã cho có nghiệm khi m ≤ - 0 , 92 .
Mặt khác m nguyên và m ∈ - 20 ; 20 vì vậy m = - 19 ; - 18 ; . . . ; - 1 nên có 19 giá trị m cần tìm.
Đáp án B.

Câu 1:
Đặt \(3^x=t(t>0)\)
PT trở thành:
\(t^2-6.t+5=m\)
\(\Leftrightarrow t^2-6t+(5-m)=0\)
Để PT có đúng một nghiệm thì \(\Delta'=9-(5-m)=0\)
\(\Leftrightarrow m=-4\)
Thử lại \(9^x-6.3^x+9=0\Leftrightarrow 3^x=3\Leftrightarrow x=1\in [0;+\infty )\) (đúng)
Vậy \(m=-4\)
Câu 2:
\(4^x-2^x-m\geq 0\Leftrightarrow (2^x)^2-2^x-m\geq 0\)
Đặt \(2^x=t\Rightarrow t^2-t-m\geq 0\) với mọi \(t\in (1; 2)\)
\(\Leftrightarrow m\leq t^2-t\Leftrightarrow m\leq \min (t^2-t)\)
Xét hàm \(f(t)=t^2-t\Rightarrow f'(t)=2t-1>0\forall t\in (1;2)\)
\(\Rightarrow f(t)> f(1)=0\) với mọi \(t\in (1;2)\)
Do đó \(m\leq 0\)




https://video.vietjack.com/upload2/quiz_source1/2020/01/100-bai-trac-nghiem-ham-so-mu-va-logarit-co-loi-giai-chi-tiet-3-1-1579254891.PNG
bạn tham khảo nha