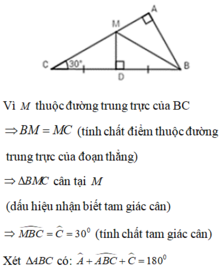
Cho Δ A B C vuông tại A, có C ^ = 30 0 , đường trung trực của BC cắt AC tại M. Em hãy chọn câu đúng:
A. BM là đường trung tuyến của Δ A B C
B. BM = AB
C. BM là phân giác của A B C ^
D. BM là đường trung trực của Δ A B C
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



a: Xét ΔABM có DN//BM
nên DN/BM=AD/AB
hay DN/CM=AD/AB(1)
Xét ΔACM có NE//MC
nên NE/MC=AE/AC(2)
Xét ΔABC có DE//BC
nên AD/AB=AE/AC(3)
Từ (1), (2) và (3) suy ra ND=NE
hay N là trung điểm của DE
=>MN là đường trung bình
b: Xét ΔNMD có \(\widehat{NMD}=\widehat{NDM}\left(=\widehat{DMB}\right)\)
nên ΔNMD cân tại N
Xét ΔMNE có NE=NM
nên ΔMNE cân tại N
Xét ΔMDE có
NM là đường trung tuyến
MN=DE/2
Do đó: ΔMDE vuông tại M

a: Xét ΔBAD vuông tại A và ΔBHD vuông tại H có
BD chung
góc ABD=góc HBD
=>ΔBAD=ΔBHD
b: ΔBAD=ΔBHD
=>BA=BH và DA=DH
=>BD là trung trực của AH
c: HD=DA(cmt)
DA<DK(ΔDAK vuông tại A)
=>HD<DK