Cho biểu thức P = − 1 3 y 2 6 m − 3 + 1 − 2 m y y + 1 2 + 1 2 y − m với m là tham số.
a) Rút gọn P.
b) Tìm y để P = 0 khi m = 1 2
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
CM
Cao Minh Tâm
24 tháng 10 2017
Đúng(0)
Những câu hỏi liên quan
2 tháng 10 2018
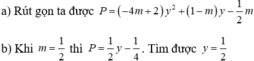
Bài 1:
a.\(\left(x+y\right)^2-\left(x-y\right)^2=\left(x+y-x+y\right)\left(x+y+x-y\right)=2\left(x+y\right)\)
b.\(2\left(x+y\right)\left(x-y\right)+\left(x+y\right)^2+\left(x-y\right)^2=\left(x+y+x-y\right)^2=4x^2\)
6 tháng 9 2021
a) \(M=a^2\left(a+b\right)-b\left(a^2-b^2\right)+1=a^3+a^2b-a^2b+b^3+1=a^3+b^3+1\)
b) \(P=x\left(x-y+1\right)-y\left(y+1-x\right)-2=x^2-xy+x-y^2-y+xy-2=x^2+x-y-y^2-2\)
c) \(Q=\left(m+3\right)\left(m^2+3m-5\right)+\left(6-m\right)m^2+11=m^3+3m^2-5m+3m^2+9m-15+6m^2-m^3+11=12m^2+4m-4\)
6 tháng 9 2021
a: Ta có: \(M=a^2\left(a+b\right)-b\left(a^2-b^2\right)+1\)
\(=a^3+a^2b-a^2b+b^3+1\)
\(=a^3+b^3+1\)
PT
8 tháng 10 2017
1.
a) \(A=\left(x-1\right)^3-\left(x+4\right)\left(x^2-4x+16\right)+3x\left(x-1\right)\)
\(A=\left(x^3-3x^2+3x-1\right)-\left(x^3+64\right)+\left(3x^2-3x\right)\)
\(A=x^3-3x^2+3x-1-x^3-64+3x^2-3x\)
\(A=\left(x^3-x^3\right)+\left(-3x^2+3x\right)+\left(3x-3x\right)+\left(-1-64\right)\)
\(A=-65\)
Vậy giá trị của biểu thức trên không phụ thuộc vào biến.
b) \(B=\left(x+y-1\right)^3-\left(x+y+1\right)^3+6\left(x+y\right)^2\)
\(B=\left[\left(x+y-1\right)-\left(x+y+1\right)\right].\left[\left(x+y-1\right)^2+\left(x+y-1\right).\left(x+y+1\right)+\left(x+y+1\right)^2\right]+6\left(x+y\right)^2\)
\(B=\left(x+y-1-x-y-1\right).\left[\left(x+y\right)^2-2\left(x+y\right).1+1+\left(x+y\right)^2-1+\left(x+y\right)^2+2\left(x+y\right).1+1\right]+6\left(x+y\right)^2\)
\(B=-2.\left(x^2+2xy+y^2-2x-2y+1+x^2+2xy+y^2-1+x^2+2xy+y^2+2x+2y+1\right)+6\left(x+y\right)^2\)
\(B=-2.\left(3x^2+6xy+3y^2+1\right)+6\left(x+y\right)^2\)
\(B=-2.\left(3x^2+6xy+3y^2\right)-2+6\left(x+y\right)^2\)
\(B=-6\left(x+y\right)^2+6\left(x+y\right)^2-2\)
\(B=-6\left[\left(x+y\right)^2-\left(x+y\right)^2\right]-2\)
\(B=-2\)
Vậy giá trị của biểu thức trên không phụ thuộc vào biến.
2. \(A=x^2+6x+11\)
\(A=x^2+2x.3+3^2+2\)
\(A=\left(x+3\right)^2+2\)
Ta có: \(\left(x+3\right)^2\ge0\)
\(\Rightarrow\left(x+3\right)^2+2\ge2\)
\(\Rightarrow Min_A=2\Leftrightarrow x=-3\)
\(B=4-x^2-x\)
\(B=-x^2-x+4\)
\(B=-x^2-x-\dfrac{1}{4}+\dfrac{17}{4}\)
\(B=-\left(x^2+2x.\dfrac{1}{2}+\dfrac{1}{4}\right)+\dfrac{17}{4}\)
\(B=-\left(x+\dfrac{1}{2}\right)^2+\dfrac{17}{4}\)
Ta có: \(-\left(x+\dfrac{1}{2}\right)^2\le0\)
\(\Rightarrow-\left(x+\dfrac{1}{2}\right)^2+\dfrac{17}{4}\le\dfrac{17}{4}\)
\(\Rightarrow Max_B=\dfrac{17}{4}\Leftrightarrow x=-\dfrac{1}{2}\)
2 tháng 10 2017
Bafi1:
\(\left(3x+4\right)\left(9x^2-12x+16\right)=65\)
<=>\(27x^3+64=65\)
=>\(27x^3=1\)
=>\(x^3=\dfrac{1}{27}\)
=>\(x=\dfrac{1}{3}\)
Vậy...
Bafi2:
\(M=\left(x+y-1\right)^3-\left(x+y+1\right)^3+6\left(x+y\right)^2\)
\(=-2-6x^2-12xy-6y^2+6\left(x^2+2xy+y^2\right)\)
\(=-2\)
Vậy...(đpcm)