Question

[Pham Trong Bach]

Cho hàm số $f\left(x\right)=\frac{x^3}{3}+(4-m)\frac{x^2}{2}+(5-2m)x+m^2+3,$ với m là tham số thực. 
 Hàm số  $g\left(x\right)=\frac{x^2+4x+5}{x+2}$ có đồ thị C và bảng biến thiên sau:

Tìm m sao cho hàm số f(x)  đạt cực trị ít nhất tại một điểm mà điểm đó lớn hơn -1

A. m> 2

B. 

C. m < -5/2 

D. m>  $\frac{5}{2}$

Answer 1

[Cao Minh Tâm]

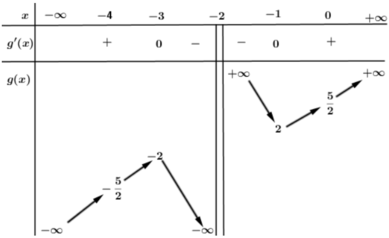
Xét phương trình f’ (x) = x²+(4-m) x+5-2m=0

⇔ x 2 + 4 x + 5 = m ( x + 2 ) ⇔ g ( x ) = x 2 + 4 x + 5 x + 2 = m

Ta có nghiệm của f’ (x)=0 cũng là hoành độ giao  điểm của g(x)=m

Khi đó từ bảng biến thiên ta có YCBT khi m>  2.

Chọn A.