Cho hình chóp S.ABC có SA=BC=2a. Gọi M, N lần lượt là trung điểm của AB, và SC, M N = a 3 . Tính số đo góc giữa hai đường thẳng SA và BC
A. 30⁰.
B. 150⁰.
C. 60⁰.
D. 120⁰.
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Ta có {BC⊥ABAB⊥SC⇒AB⊥CE{BC⊥ABAB⊥SC⇒AB⊥CE
Khi đó {CE⊥ABCE⊥SA⇒CE⊥(SAB){CE⊥ABCE⊥SA⇒CE⊥(SAB)
Áp dụng hệ thức lượng trong tam giác vuông ta có: SC2=SE.SB⇒SESB=SC2SB2SC2=SE.SB⇒SESB=SC2SB2, tương tự SDSE=SC2SA2SDSE=SC2SA2
Lại cả CA=AC√2=2a;VS.ABC=13SC.SABC=23a3CA=AC2=2a;VS.ABC=13SC.SABC=23a3
Khi đó VS.CDEVS.ABC=SESBSDSA=SC2SB2.SC2SA2=4648=13VS.CDEVS.ABC=SESBSDSA=SC2SB2.SC2SA2=4648=13
Do đó VS.CDE=13.23a3=2a39VS.CDE=13.23a3=2a39.

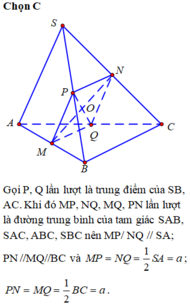
Gọi D là hình chiếu vuông góc của S lên (ABC)
\(SD\perp\left(ABC\right)\Rightarrow SD\perp AB\) , mà \(AB\perp SA\left(gt\right)\Rightarrow AB\perp\left(SAD\right)\Rightarrow AB\perp AD\)
\(\Rightarrow AD||BC\)
Tương tự ta có: \(BC\perp\left(SCD\right)\Rightarrow BC\perp CD\Rightarrow CD||AB\)
\(\Rightarrow\) Tứ giác ABCD là hình vuông
\(\Rightarrow BD=a\sqrt{2}\)
\(SD=\sqrt{SB^2-BD^2}=a\sqrt{2}\)
Gọi P là trung điểm AD \(\Rightarrow MP\) là đường trung bình tam giác SAD
\(\Rightarrow\left\{{}\begin{matrix}MP=\dfrac{1}{2}SD=\dfrac{a\sqrt{2}}{2}\\MP||SD\Rightarrow MP\perp\left(ABC\right)\end{matrix}\right.\)
\(\Rightarrow\alpha=\widehat{MNP}\)
\(cos\alpha=\dfrac{NP}{MN}=\dfrac{NP}{\sqrt{NP^2+MP^2}}=\dfrac{a}{\sqrt{a^2+\dfrac{a^2}{2}}}=\dfrac{\sqrt{6}}{3}\)

Đáp án A.
Phương pháp:
- Phương pháp tọa độ hóa.
- Công thức tính khoảng cách giữa hai đường thẳng trong không gian:
d Δ 1 ; Δ 2 = M 1 M 2 → . u 1 → ; u 2 → u 1 → ; u 2 → , M 1 ∈ Δ 1 ; M 2 ∈ Δ 2
Cách giải:
Gắn hệ trục tọa độ (như hình vẽ):
A 0 ; 0 ; 0 , B 0 ; a ; 0 , C a 3 2 ; a 2 ; 0 , S 0 ; 0 ; 3 a
M, N lần lượt là trung điểm của AB, SC
⇒ M 0 ; a 2 ; 0 , N a 3 4 ; a 4 ; 3 a 2
⇒ A N → = a 3 4 ; a 4 ; 3 a 2 ; C M → = − a 3 2 ; 0 ; 0
Đường thẳng AN có 1 VTCP u 1 → = 3 ; 1 ; 6 ,
đi qua điểm A 0 ; 0 ; 0 .
Đường thẳng CM có 1 VTCP u 1 → = 1 ; 0 ; 0 , đi qua điểm A 0 ; a 2 ; 0 .
A M → = 0 ; a 2 ; 0 , u 1 → ; u 2 → = 0 ; 6 ; − 1
d A N ; C M = A M → . u 1 → ; u 2 → u 1 → ; u 2 → = 0.0 + a 2 .6 + 0. − 1 0 2 + 6 2 + 1 2 = 3 a 37

Đáp án là C.
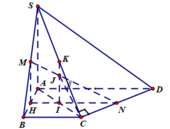

Ta dễ chứng minh được tam giácACD vuông tại C, từ đó chứng minh được CN vuông góc với mặt phẳng (SAC) hay C là hình chiếu vuông góc của N trên (SAC). Đường thẳng MN cắt mặt phẳng (SAC) tại J xác định như hình vẽ. Suy ra góc giữa MN và (SAC) là góc NJC .
IN là đương trung bình trong tam giác ACD suy ra IN=a, IH là đường trung bình trong tam giác ABC suy ra I H = 1 2 B C = a 2 . Dựa vào định lí Talet trong tam giác MHN ta được I J = 2 3 M H = 2 3 . 1 2 S A = 1 3 S A = a 3 . Dựa vào tam giác JIC vuông tại I tính được J C = 22 6 .
Ta dễ tính được C N = a 2 2 , J N = a 10 3 .
Tam giác NJC vuông tại C nên cos N J C ^ = J C J N = 55 10 .