Cho hình thang ABCD, đáy nhỏ AB. Gọi M, N, P, Q lần lượt là trung điểm của AD, BD, AC, BC. Khi đó NP có độ dài bằng?
A. A B 2 ;
B. C D 2 ;
C. A B + C D 2 ;
D. C D − A B 2 .
K
Khách
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Những câu hỏi liên quan
9 tháng 9 2021
b: Xét ΔABD có
M là trung điểm của AB
Q là trung điểm của AD
Do đó: MQ là đường trung bình của ΔBAD
Suy ra: MQ//BD và \(MQ=\dfrac{BD}{2}\left(1\right)\)
Xét ΔBCD có
N là trung điểm của BC
P là trung điểm của CD
Do đó: NP là đường trung bình của ΔBCD
Suy ra: NP//BD và \(NP=\dfrac{BD}{2}\left(2\right)\)
Từ (1) và (2) suy ra NP//MQ và NP=MQ
Xét ΔADC có
Q là trung điểm của AD
P là trung điểm của CD
Do đó: QP là đường trung bình của ΔADC
Suy ra: QP//AC
mà AC\(\perp\)BD
nên QP\(\perp\)BD
mà MQ//BD
nên MQ\(\perp\)QP
hay \(\widehat{MQP}=90^0\)
Xét tứ giác MQPN có
MQ//NP
MQ=NP
Do đó: MQPN là hình bình hành
mà \(\widehat{MQP}=90^0\)
nên MQPN là hình chữ nhật
Xét tứ giác MQPN có
\(\widehat{MQP}+\widehat{MNP}=180^0\)
Do đó: MQPN là tứ giác nội tiếp
hay M,Q,P,N cùng thuộc 1 đường tròn
D
21 tháng 7 2021
a/
△ACD có:
- MN lần lượt đi qua trung điểm của AD và AC tại M và N
=> MN là đường trung bình của △ACD
Mặt khác, hình thang ABCD có:
- MP lần lượt đi qua trung điểm của AD và BC tại M và P
=> MP là đường trung bình của hình thang ABCD
=> MN trùng MP
Vậy: M, N, P thẳng hàng. (đpcm)
b/
- MN là đường trung bình của △ACD (cmt)
=> \(MN=\dfrac{1}{2}CD\)
Hay: \(MN=\dfrac{1}{2}.7=3,5\left(cm\right)\)
- MP là đường trung bình của hình thang ABCD (cmt)
=> \(MP=\dfrac{1}{2}AB.CD\)
Hay: \(MP=\dfrac{5+7}{2}=6\left(cm\right)\)
- \(NP=MP-MN\)
Hay: \(NP=6-3,5=2,5\left(cm\right)\)
- Nhận xét: Độ dài MP = 1/2 tổng độ dài hai đáy AB và CD
Vậy:
\(MN=3,5\left(cm\right)\)
\(NP=2,5\left(cm\right)\)
\(MP=6\left(cm\right)\)
CH
Cô Hoàng Huyền
Admin
VIP
12 tháng 3 2018
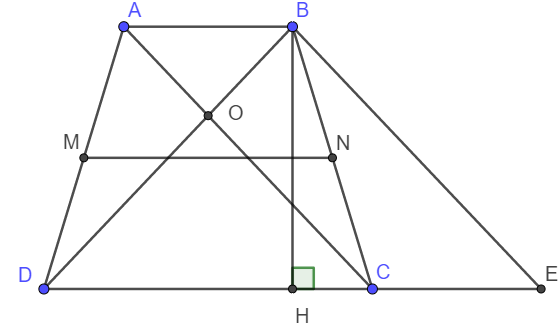
a) Xét tứ giác ABEC có AB // CE; AC // BE .
Vậy nên ABEC là hình bình hành. Suy ra AB = CE.
Do MN là đường trung bình hình thang ABCD nên ta có :
\(MN=\frac{AB+DC}{2}=\frac{CE+DC}{2}=\frac{DE}{2}.\)
b) Do ABCD là hình thang cân nên ta có:
\(AD=BC;DB=AC\)
Xét tam giác ABD và tam giác BAC có:
Cạnh AB chung
AD = BC
BD = AC
\(\Rightarrow\Delta ABD=\Delta BAC\left(c-c-c\right)\)
\(\Rightarrow\widehat{ABD}=\widehat{BAC}\) hay \(\widehat{ABO}=\widehat{BAO}\)
Xét tam giác OAB có \(\widehat{ABO}=\widehat{BAO}\) nê OAB là tam giác cân tại O.
c) Do ABEC là hình bình hành nên AC = BE
Lại có AC = BD nên BD = BE
Suy ra tam giác BDE cân tại B.
Tam giác cân BDE có BH là đường cao nên đồng thời là đường trung tuyến.
Lại có theo câu a thì MN = DE/2
Giả thiết lại cho MN = BH. Vậy nên BH = DE/2
Xét tam giác BDE có trung tuyến BH bằng một nửa cạnh tướng ứng nên BDE là tam giác vuông tại B.
Vậy BDE là tam giác vuông cân tại B.
5 tháng 10 2021
a,Vì \(\left\{{}\begin{matrix}AM=MD\\BQ=QC\end{matrix}\right.\) nên MQ là đtb hình thang ABCD \(\Rightarrow MQ//AB\left(1\right)\)
Vì \(\left\{{}\begin{matrix}AM=MD\\DN=NB\end{matrix}\right.;\left\{{}\begin{matrix}BQ=QC\\AP=PC\end{matrix}\right.\) nên MN,PQ lần lượt là đtb các tam giác ABD,ABC
\(\Rightarrow MN//AB\left(2\right);PQ//AB\left(3\right)\)
Từ \(\left(1\right)\left(2\right)\left(3\right)\Rightarrow MN;MQ;PQ\) trùng nhau hay M,N,P,Q thẳng hàng
b,Ta có \(NP=MQ-MN-PQ\)
\(\Rightarrow NP=\dfrac{AB+CD}{2}-\dfrac{AB}{2}-\dfrac{AB}{2}\left(t/c.đường.trung.bình\right)\\ \Rightarrow NP=\dfrac{CD-AB}{2}\)
Đáp án D